Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 57

57 . || Um bloco de massa m parte do repouso de uma altura h . Ele desce deslizando sobre uma rampa sem atrito, atravessa uma superfície horizontal áspera de comprimento L e, então, começa a subir por outra rampa, livre de atrito. O coeficiente de atrito cinético da superfície áspera é   μ e .

a. Quanto vale a velocidade do bloco na base da primeira rampa?

b. Até que altura o bloco sobe na segunda rampa?

Expresse suas respostas em função de m , h , L , μ e e g .

Passo 1

Um esquema e desenho é:

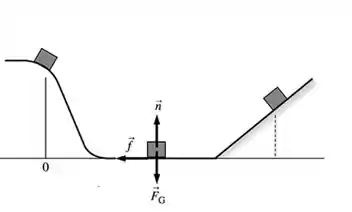
Essa é uma questão aberta, não encontraremos valores numéricos e sim deduziremos fórmulas em função de m , h , L , μ e e g .!

Passo 2

a. Quanto vale a velocidade do bloco na base da primeira rampa?

Usando a conservação de energia:

m g h = 1 2 m v 0 2

v 0 = 2 g h  

Passo 3

b. Até que altura o bloco sobe na segunda rampa?

O atrito cria energia e retira parte da energia cinética. Aplicando mais uma vez a equação de conservação de energia, para energia cinética E c temos:

E c = 1 2 m v 0 2 - f a t r i t o L

E c = 1 2 m 2 g h 2 - μ e m g L

E c = m g h - μ e L

O que sobrou será igual a Energia potencial:

E P o t = m g h - μ e L

m g h 2 = m g h - μ e L

h 2 = h - μ e L

Resposta

( a )

v 0 = 2 g h  

( b )

h 2 = h - μ e L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A única força que age sobre um corpo de 2,0k g quando o corpo se desloca ao longo de um eixo x varia da forma indicada na Fig. 7-42. A escala vertical do gráfico é definida por F s = 4,0N . A velocida
Se um carro com uma massa de 1200k g viaja a 120k m / h em uma rodovia, qual é a energia cinética do carro medida por alguém que está parado no acostamento?
Um trenó à vela está em repouso sobre a superfície de um lago congelado quando um vento repentino exerce sobre ele uma força constante de 200N , na direção leste. Devido ao ângulo da vela, o vento faz
A única força que age sobre uma lata de 2,0k g que está se movendo em um plano x y tem um módulo de 5,0N . Inicialmente, a lata tem uma velocidade de 4,0m / s no sentido positivo do eixo x ; em um ins
A Fig. 7-27 mostra três forças aplicadas a um baú que se desloca 3,00m para a esquerda sobre um piso sem atrito. Os módulos das forças são F 1=5,00N , F 2=9,00N e F 3=3,00N ; o ângulo indicado é θ=60