Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.Problemas Adicionais - Ex. 66
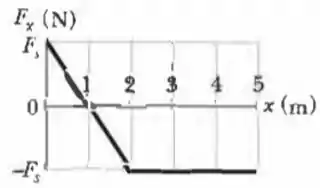
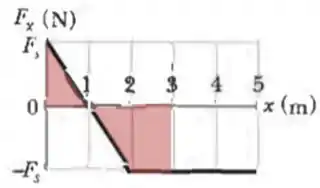
A única força que age sobre um corpo de quando o corpo se desloca ao longo de um eixo varia da forma indicada na Fig. 7-42. A escala vertical do gráfico é definida por . A velocidade do corpo em é . (a) Qual é a energia cinética do corpo em ? (b) Para que valor de o corpo possui uma energia cinética de ? (c) Qual é a energia cinética máxima do corpo entre e ?
Passo 1
Oi, galerinha! Tudo bom? Para resolver essa questão devemos ter em mente o teorema trabalho-energia cinética que diz:
Entao repara que se achamos o trabalho, nós temos a energia cinética.
Agora vamos olhar para o gráfico! Repara que a área do gráfico de em função de é igual ao trabalho (). Portanto, nesta questão, iremos dividir o gráfico em figuras que conhecimentos a fórmula da área para determinar o trabalho.
Passo 2
- Para determinar a energia cinética do corpo em , vamos calcular o trabalho de até e, por fim, usar o teorema trabalho-energia cinética.
- Para determinar o valor de que o corpo possui uma energia cinética de , faremos o processo contrário ao que foi feito nos passos anteriores. Primeiro determinaremos a variação da energia cinética e, após essa etapa, aplicaremos o teorema trabalho-energia cinética. Considerando de até :
- Para determinar a energia cinética máxima , devemos lembrar que a energia cinética aumenta quando o trabalho é positivo, como só temos trabalho positivo de até , então a energia cinética máxima ocorrerá em . Portanto, aplicando o teorema trabalho-energia cinética entre os pontos citados:
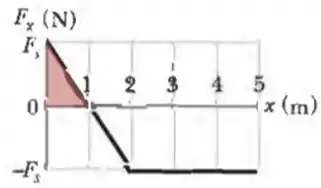
Calculando a área do primeiro triângulo formado de até :
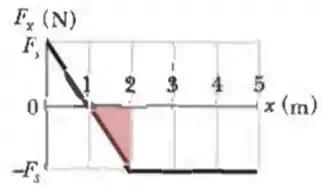
Para o segundo triângulo formado de até , lembrando que como ele está no semieixo negativo, então o trabalho será negativo:
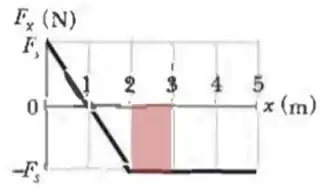
Para o retângulo formado de até , também negativo:
Então, o trabalho total de até é:
Passo 3
Com o trabalho calculado de até , podemos usar a para determinar a energica cinética em (), tendo em vista que o problema nos deu a velocidade inicial e a massa do corpo. Assim:
Isolando :
Passo 4
Aplicando agora o teorema trabalho-energia:
Aqui, devemos lembrar que já calculamos o trabalho realizado de até , portanto, podemos reescrever a expressão acima:
O pulo do gato agora é perceber que a força que atua nesse corpo de em diante é constante e calculando o trabalho usando a área do gráfico a partir de :
Isolando :
Passo 5
O trabalho já foi calculado em passos anteriores, assim como , então devemos agora substituir os valores:
Resposta
- ;
- ;
- .