Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 66
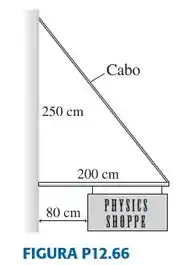
|| Uma placa com de largura está suspensa por uma haste de e de comprimento. Um cabo de massa desprezível sustenta a extremidade da haste, como mostrado na . Qual é o máximo valor de massa que a placa pode ter se a tensão máxima que o cabo suporta sem se romper é de ?
Passo 1
Da figura podemos esquematizar e desenhar algumas coisas:
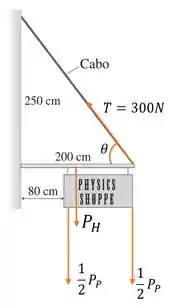
é o peso da haste.
é peso da placa.
O ângulo é:
Passo 2
Calculando o torque e igualando a zero pois está em equilíbrio.
Resposta
Exercícios de Livros Relacionados
60 . || Calcule o momento de inércia da chapa de aço da F I G U R AP 12.53 para rotações em torno de um eixo perpendicular à chapa e que passa pela origem.
58. || a . Um disco de massaM e raio R tem um buraco de raio r centrado no eixo de simetria. Calcule o momento de inércia do disco. b . Confirme se sua resposta concorda com a T a b e l a12.2 quando r
8 . A Figura PO 10.8 mostra um sistema de quatro partículas unidas por barras leves e rígidas. Suponha que a=b e M seja maior que m . Ao redor de quais eixos coordenados o sistema tem ( i ) o menor e
Determine o momento de inércia da área sombreada em relação ao eixo x .
Determine o momento de inércia da área sombreada em relação ao eixo y .