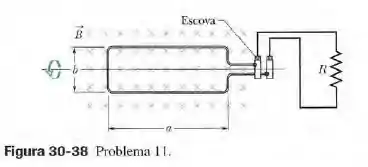
Uma bobina retangular de comprimento e largura , com espiras, gira com frequência na presença de um campo magnético uniforme , como mostra a figura 30-38. A bobina está ligada a cilindros metálicos que giram solidariamente a ela e nos quais estão apoiadas nas escovas metálicas que fazem contato com um circuito externo. (a) Mostre que a força eletromotriz induzida na bobina é dada (em função do tempo ) pela equação

Este é o princípio de funcionamento dos geradores comerciais de corrente alternada. (b) para que valor de a força eletromotriz gerada tem uma amplitude quando a bobina gira com uma frequência de revoluções por segundo em um campo magnético uniforme de ?

Bom, galera, um cara chamado Faraday descobriu que uma força eletrmotriz e uma corrente podem ser induzidas em uma espira fazeno variar a quantidade de campo magnético que atravessa a espira. Ele ainda percebeu que a dita “quantidade de campo magnético” pode ser visualizada em termos das linhas de campo magnético que atravessam a espira.

O número de linhas que atravessam a espira não importa; os valores da força eletromotriz e da corrente induzida são determinados pela taxa de variação desse número. O módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:

O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.

Pessoal, convém chamar atenção para o fato de que o resultado, que está expresso em termos de , poderia, em vez disso, estar expresso em termos de ou mesmo de , em que é uam constante de fase. A posição angular da bobina é medida em relação a uma reta ou pllano de referência e, de acordo com a escolha, o fluxo magnético pode ser dado como . Para a referência que foi escolhida, o nosso fluxo magnético será dado por . Como a bobina está girando com velocidade angular constante, aumenta linearmente com o tempo. Assim, , em que é o ângulo em radianos e a velocidade angular. Como a área de uma bobina retangular é , a lei de Faraday nos dá:

que é justamente a equação que queríamos demonstrar. No enunciado, a equação também é escrita de outra forma, , para deixar claro que a fem induzida é senoidal e tem uma amplitude .