Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 60
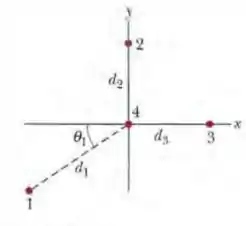
Na Fig , determine o módulo e a orientação da força eletrostática total a que está submetida a partícula . Todas as partículas são mantidas fixas no plano ; ; ; ; ; ;
Passo 1
Fala aí, pessoal! 😊
Nesse problema temos um sistema com partículas carregadas em que ; ; ; ; ; e nosso objetivo é obter o modulo e a orientação da força eletrostática que a partícula sofre.
Lembra como fazemos isso? 🤔
A força elétrica entre duas partículas é dada por:
Onde e as interações das cargas em e geram vetores no ponto como pode ser visto na figura abaixo:
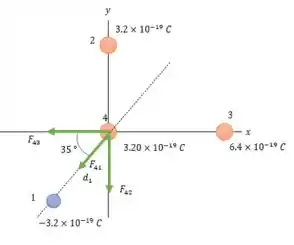
Veja só! 😉
Passo 2
Então a força total exercida na partícula será:
Sabendo que as distâncias entre as partículas são:
Então encontrando as forças nós temos:
Orientação negativa em pois como as cargas 3 e 4 tem polos positivo então temos uma força de repulsão. Que na carga estará orientada para baixo em .
Mesma coisa, as cargas 4 e 3 tem cargas positivas então a força em 4 será de repulsão, direcionada para negativo no eixo .
A direção de pode ser mais complicada, mas pega a visão:
Nesse caso temos que projetar o vetor resultante nos dois eixos, o que nos dá no eixo e no eixo , já que nesse caso a força é de atração entre os corpos 1 e 4.Então:
Fazendo então a soma para encontrar a força no corpo 4 nós temos:
Somando com e com nós temos:
Tranquilo até aqui? 😉
Passo 3
Então o módulo da força no corpo 4 será igual a:
E vendo que tanto a força projetada em quanto a força projetada em são negativas então o ângulo de orientação da força resultante está no terceiro quadrante de forma que:
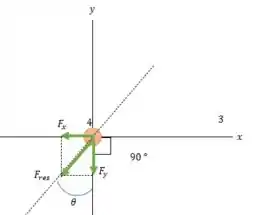
Portanto o ângulo de orientação da força resultante com o eixo positivo será de:
E aí! entendeu tudo? Responde Aí! 😁
