Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.4 - Ex. 10

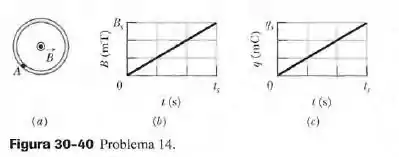
Na figura 30-40a, o módulo do campo magnético uniforme aumenta com o tempo de acordo com o gráfico da figura 30-40b, onde a escala do eixo vertical é definida por e a escala do eixo horizontal é definida por Uma espira circular com uma área de , no plano do papel, é submetida ao campo. A figura 30-40c mostra a carga que passa pello ponto a espira em função do tempo , com a escala do eixo vertical definida por e a escala do eixo horizontal definida novamente por . Qual é a resistência da espira?

Passo 1

Bom, galera, o módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:

O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.

De acordo com a figura 30-40b, o valor de , que seria a inclinação da reta que representa a função , é igual a . Assim, pela lei de Faraday:

Passo 2

Agora vamos olhar para a figura 30-40c. Nela vemos que o valor da corrente é a inclinação da reta que representa a função q(t) e é igual a . Assim, a lei de Ohm nos dá:

Resposta

A resistência da espira é:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É impossível existir um campo elétrico uniforme que caia repentinamente até zero em uma região do espaço onde o campo magnético é uniforme e constante. Para provar essa afirmação, use o método da cont

Em uma região do espaço onde não há corrente de condução nem de deslocamento, é impossível existir um campo elétrico uniforme que caia repentinamente até zero. Para comprovar essa afirmação, use o mét

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para

15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário

16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .