51. Uma bola (de ) é lançada do teto de um edifício, acima do chão. Sua velocidade inicial é de , formando acima da horizontal. Despreze a resistência do ar.

a) Qual a altura máxima, acima do chão, atingida pela bola?

a) A figura abaixo mostra a bola sendo lançada do telhado do edifício. Vamos considerar nosso sistema de análise como formado pela bola e pela terra. Então, O trabalho da força externa, , é igual a zero. Escolhemos no nível do solo e podemos então usar conservação de energia mecânica para determinar a altura máxima da bola.

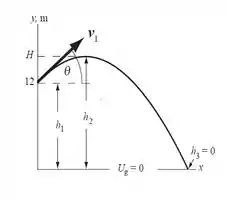
Temos então os seguintes dados:

= altura inicial da bola

= altura máxima da bola

= altura final da bola

= velocidade de lançamento

Sabemos, lá do lançamento oblíquo de projéteis, que na altura máxima, a velocidade não é nula, mas igual a componente horizontal da velocidade de lançamento, . Temos então, nesse instante energia cinética e potencial gravitacional. O mesmo ocorre para o instante inicial, já que o lançamento ocorre a uma altura e obviamente, com uma determinada velocidade.

O que temos que fazer é igualar as energias no instante , de lançamento, e , de altura máxima.

Chamando as energias potencial e cinética em de e , e em , de e ; vamos então igualá-las de acordo com o princípio da conservação da energia mecânica.

Vamos então usar as fórmulas relativas a cada tipo de energia:

Só que , lá na altura máxima, nada mais é do que a componente horizontal da velocidade de lançamento dada por . Logo, susbtituindo na relação de antes:

Substituímos os valores numéricos correspondentes e chegamos a: