Uma bola de aço de e outra, também de aço e com , estão suspensas por barbantes de de comprimento. Em repouso, as bolas situam-se lado a lado, mal se tocando. A bola de é puxada para a esquerda até que seu barbante forme 45° com a vertical. A bola de é puxada em para a direita. As bolas são liberadas de modo que colidem exatamente no ponto mais baixo de suas oscilações. Até que ângulo cada bola ricocheteia?
Passo 1
Se liga! Ao afastarmos uma bola da outra, conforme fala o enunciado, temos a configuração mostrada na figura.
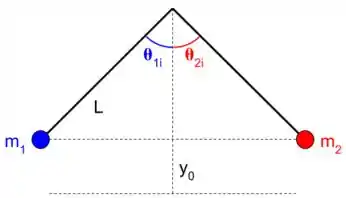
Onde
Na hora da colisão todos fios se encontram praticamente na vertical, conforme mostrado na figura a seguir.
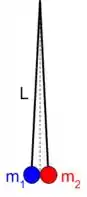
A diferença de altura entre as bolas na posição inicial e no instante em que colidem é dada por
Passo 2
Para descobrir a velocidade com que a bola 1 chega no ponto de colisão, podemos usar a conservação da energia mecânica. Levando em consideração que antes de começar a cair a bola só possui energia potencial gravitacional e o instante da colisão apenas energia cinética, podemos escrever que
Isolando e substituindo o , temos
Substituindo os valores encontramos
Passo 3
Considerando que a bola 2 cai a partir da mesma altura e vimos que o cálculo independe da massa, podemos dizer que chegará no ponto de colisão com a mesma velocidade. Mas em sentido oposto.
Passo 4
Sabemos que na colisão o momento linear deve se conservar.
O momento linear no início é dado por
O momento depois da colisão é dado por
Igualando, temos
Multiplicando os dois lados por 10 e isolando , temos
Passo 5
Considerando que a colisão seja elástica diremos que a energia cinética deve se conservar.
Antes da colisão temos que
Depois da colisão temos
Igualando temos
Substituindo (1) em (2), temos
Resolvendo esta equação encontramos duas soluções
Como o primeiro resultado representa o mesmo valor da velocidade dessa bola antes da colisão, o que não faz sentido, pois a bola muda o seu sentido, consideraremos o segundo resultado. Substituindo este na equação (1), temos
Passo 6
Agora precisamos encontrar os ângulos, para isso usaremos a conservação da energia mecânica.
Se liga na nova configuração.
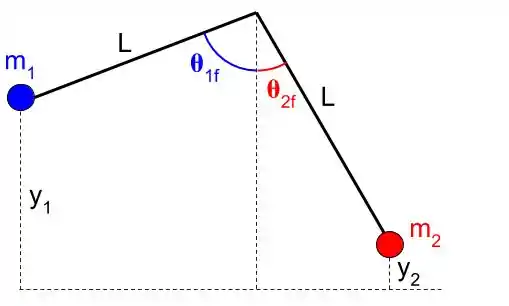
Para cada uma das bolas, temos
Podemos achar e da mesma forma que achamos . Portanto
Agora vamos substituir essas expressões para a bola 1, temos
Para a bola 2, temos
Passo 7
Agora só precisamos aplicar o arcosseno e substituindo os valores.