Uma vara uniforme, de de comprimento, é elevado a com a horizontal em cima de uma camada de gelo. A extremidade de baixo da vara permanece apoiada sobre o gelo. A vara é largada do repouso. A extremidade de baixo permanece sempre em contato com o gelo. Qual será a distância percorrida pela extremidade de baixo, durante o tempo em que o resto da vara cai sobre o gelo? Suponha o gelo sem atrito.
Passo 1
Como não tem forças horizontais atuando, o centro de massa vai ficar imóvel na direção horizontal. É uma boa escolhermos um sistema de coordenadas cuja origem seja na posição horizontal do centro de massa.
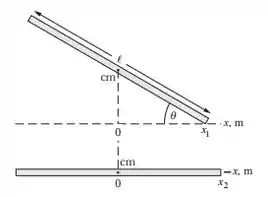
Passo 2
O deslocamento da ponta direita da vara vai ser:
Não esquece! O centro de massa de uma barra homogênea é no seu ponto médio!
Usando trigonometria na figura, vamos encontrar:
Como o centro de massa não se move na figura, vai ser igual a metade da barra.
Passo 3
Logo,