Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.4 - Ex. 60
Uma bola de boliche de 71,2 N está presa ao teto por uma corda de . Abola é empurrada para um lado e libertada; ela então oscila para frente e para trás, como um pêndulo. Quando a corda passa pela vertical, a velocidade da bola é igual a 4,20 m/s.
a) Qual é o módulo, a direção e o sentido da aceleração da bola nesse instante? b) Qual é a tensão na corda nesse instante?
Passo 1
O bola de boliche tem aceleração centrípeta, , direcionada para o centro do caminho circular. Quando a bola está na parte inferior do balanço, sua aceleração é para cima.
Sabemos que a aceleração centrípeta é:
Vamos considerar como para cima, na direção da aceleração.
A massa da bola de boliche se dá por:
Passo 2
- Pelo enunciado, sabemos que o raio, , é o comprimento da corda presa a bola de boliche, ou seja, . E que a velocidade é .
Agora basta calcular:
Para cima.
Passo 3
Vamo considerar um diagrama de corpo livre para bola de boliche:
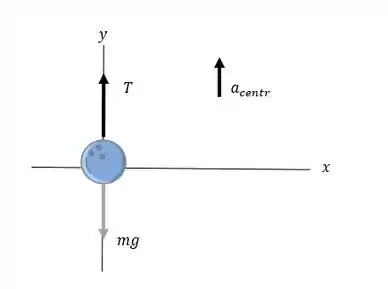
Como a bola está ligada a um fio, temos uma tração, , agindo nesse sistema. A bola está suspensa, e não encosta em nada que aja como a força normal, .
Então, vamos aplicar a segunda lei de Newton sobre a bola de boliche ao , já que é o único eixo do qual temos forças atuando:
A aceleração é para cima, então a força resultante é para cima e a tensão é maior que o peso.
No limite da perda de contato a normal tende a zero: .