Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.4 - Ex. 57
Um avião faz uma volta circular em um plano vertical (um loop) com um raio de . A cabeça do piloto sempre aponta para o centro do círculo. A velocidade do avião não é constante; o avião vai mais devagar no topo do círculo e tem velocidade maior na base do círculo. a) No topo do círculo, o piloto possui peso aparente igual a zero. Qual é a velocidade do avião nesse ponto? b) Na base do círculo, a velocidade do avião é de . Qual é o peso aparente do piloto nesse ponto? O peso real do piloto é de .
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um avião faz uma volta circular em um plano vertical (um loop) com um raio de .
A cabeça do piloto sempre aponta para o centro do círculo.
A velocidade do avião não é constante; o avião vai mais devagar no topo do círculo e tem velocidade maior na base do círculo.
Queremos calcular a velocidade do avião no topo do círculo, ou seja, quando o piloto possui peso aparente igual a zero.
Também queremos o peso aparente do piloto na base do círculo, quando a velocidade do avião é de .
O enunciado ainda nos dá como o dado o peso real de do piloto.
Bom... Nessa questão temos um piloto que se move em um círculo vertical. Então é uma questão de movimento circular!
O peso aparente é a força normal exercida sobre ele. Em cada ponto a aceleração centrípeta é direcionada para o centro do caminho circular e ela é dada por:
Onde é a velocidade e é o raio.
Vamos lá olhar cada item!
Passo 2
a) Nessa situação, o piloto está na parte mais alta da trajetória, e “o peso aparente é zero”, ou seja, a força normal vertical, , exercida sobre o piloto pela cadeira qual o piloto senta é zero.
Vamos esboçar o diagrama de corpo livre dessa situação:
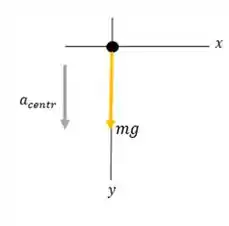
Observe que só temos forças agindo no , e que não temos uma normal, , pois esta é nula.
Temos somente a força peso agindo e que vale .
Colocamos também no diagrama a aceleração centrípeta. Ela aponta para baixo, em direção ao centro do circulo descrito pelo avião.
Passo 3
Então, vamos aplicar a segunda lei de Newton para verificar o somatório das forças em desse caso:
Onde é a massa e é a aceleração.
Temos uma expressão para , substituindo
Isolando , chegamos a:
Substituindo e .
Para converter para , basta mutplicarmos a velocidade por
Passo 4
b) Queremos achar o peso aparente, que é a força normal exercida sobre o piloto pela cadeira.
Agora, vamos esboçar o diagrama de força para o piloto na parte inferior da trejetória.
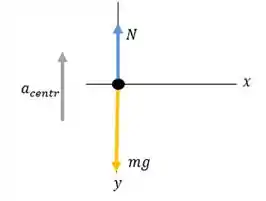
Note que a força normal é exercida no piloto pela cadeira em que o piloto está sentado e esta aponta para cima.
A aceleração centrípeta está para cima apontando para o centro da trajetória circular. E temos a força peso do piloto .
Passo 5
Então, vamos aplicar a segunda Lei de Newton no , uma vez que só temos forças atuando nesse eixo:
Essa força normal, , é o peso aparente do piloto.
Passo 6
Sabemos que o peso, , é:
Então:
Sabendo que o peso real do homem é e :
Passo 7
Agora, temos uma velocidade, , em e precisamos converter para para que possamos usar todos os resultados encontrados para calcular a normal, .
Basta dividirmos essa velocidade por
Passo 8
Prontooooo!
Agora podemos substituir os valores na equação da normal, , que encontramos no passo 3.
A normal, , que vamos encontrar será o peso aparente do piloto nesse ponto.