Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 5.Problemas - Ex. 16
O coeficiente de atrito estático entre as roupas de uma pessoa e a parede cilíndrica de uma centrífuga de parque de diversões de 2m de raio é 0,5. Qual é a velocidade angular mínima (em rotações por minuto) da centrífuga para que a pessoa permaneça colada à parede, suspensa acima do chão?
Passo 1
Vamos partir pro nosso esqueminha de forças pra gente visualizar o que acontece, belê?
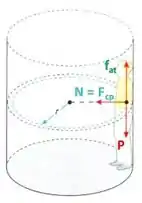
A força que nos faz girar juntamente com a centrífuga é a normal da parede, responsável por formar o atrito estático que nos segura contra a gravidade, nossa equação de equilíbrio fica
O atrito é estático, então
Como a normal é a resultante centrípeta, temos
Finalmente, bora cortar as massas e isolar a velocidade angular
Pronto, agora é só passar pra unidade pedida, show? Se 1 volta tem então 3,13 representa voltas. Ou seja, nossa velocidade é de . Já que queremos a quantidade de voltas por minuto é só multiplicar por 60.