Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 17

Uma bola de boliche esférica uniforme é lançada, com velocidade v 0 horizontal e sem rotação inicial, sobre uma cancha horizontal, com coeficiente de atrito cinético μ c .

(a) Que distância d a bola percorrerá até que comece a rolar sem deslizar?

(b) Quanto tempo t depois do lançamento isso ocorre?

(c) Qual é a velocidade v da bola nesse instante?

Passo 1

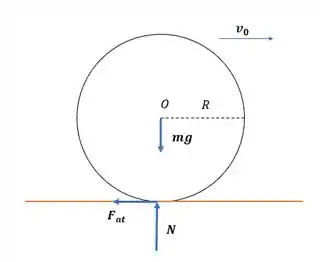
Primeiro vamos escrever as equações de Newton para a bola de boliche.

No eixo y :

N - m g = 0 → N = m g

No eixo x :

- f a t = m a

Usando que f a t = μ c N e N = m g :

a = - μ c g     ( i )

Passo 2

Agora vamos analisar a rotação da bola. Calculando torque com relação ao centro:

τ = F a t R

Como τ = I α :

μ c m g R = I α

Para a bola de boliche I = 2 5 m R 2 , logo:

μ c m g R = 2 5 m R 2 α

Assim,

α = 5 2 μ g R

Como inicalmente ω 0 = 0 . Então,

ω t = α t = 5 μ c g 2 R t     ( i i )

Passo 3

Agora precisamos juntar as duas coisas. Como queremos o caso em que ele rola sem deslizar.

v = ω R       ( i i i )

Da equação ( i ) :

v = v 0 + a t → v = v 0 - μ c g t

Juntando com a equação ( i i ) e substituindo em ( i i i ) :

v 0 - μ c g t = 5 μ c g 2 R t R

Então,

t = 2 v 0 7 μ c g

A velocidade nesse ponto será:

v = v 0 - μ c g ⋅ 2 v 0 7 μ c g = 5 v 0 7

Por fim, a distância percorrida será:

v 2 = v 0 2 - 2 μ c g Δ d

Logo,

Δ d = ( v 0 2 - 25 v 0 2 49 ) / ( 2 μ c g )

Portanto,

Δ d = 12 v 0 2 49 μ c g

Resposta

  1. Δ d = 12 v 0 2 49 μ c g

  2. t = 2 v 0 7 μ c g

  3. v = 5 v 0 7
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco sólido rola sem deslizar sobre uma superfície horizontal com velocidade constante de 2,50 m/s. a) Se o disco rola para cima de uma rampa inclinada a 30,0º, qual é a distância máxima que ele a
O ioiô. Um ioiô é feito usando-se dois discos uniformes, cada um com massa m e raio R ligados por um eixo leve de raio b. Um fio leve e fino é enrolado diversas vezes em torno do eixo e a seguir manti
Uma bola de gude homogênea rola sem deslizar para baixo da trajetória indicada na Figura 10.59, partindo do repouso. a) Ache a altura mínima h necessária para que a bola de gude não caia na cova.b) O
Uma criança faz uma bola de basquete de 0,600 kg rolar para cima de uma rampa longa. A bola de basquete pode ser considerada uma casca esférica, de paredes finas. Quando a criança larga a bola na base
Uma bola maciça e uniforme rola sem deslizar para cima de uma colina, como indica a Figura 10.61. No topo da colina, ela se move horizontalmente e cai pelo rochedo vertical. a) A que distância da base