Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 15
Uma bola homogênea de raio rola sem deslizar desde o topo de um domo hemisférico de raio . (a) Depois de percorrer que ângulo em relação à vertical a bola deixará a superfície? (b) Com que velocidade isso acontece?
Passo 1
Como queremos saber o ângulo em que a bola perde, basta acharmos o ponto em que a normal é nula.
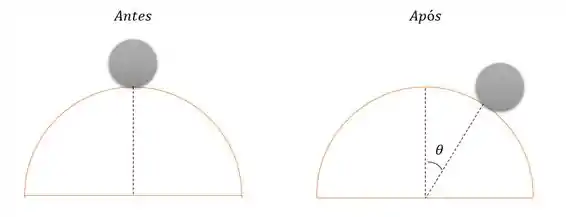Na direção radial, teremos a força centrípeta:
Como nesse ponto :
Conservando energia, temos:
Como e :
Passo 2
Arrumando as coisas, temos:
De :
Logo,
Para a velocidade, temos:
Para o :
Como :
Resposta
Exercícios de Livros Relacionados
Na Fig. 10-38, dois blocos, de massas m 1=400g e m 2 =600g , estão ligados por uma corda de massa desprezível que está enrolada na borda de um disco homogêneo de massa M = 500g e raio R=12,0cm . O dis
Uma roda de 0,20m de raio está montada em um eixo horizontal sem atrito . O momento de inércia da roda em relação ao eixo é 0,050k g .m 2 . Uma corda de massa desprezível está enrolada na roda e presa
A Figura 10.58 mostra três ioiôs idênticos que estão inicialmente em repouso sobre uma superfície horizontal. Para cada ioiô, o fio é puxado conforme indicado. Em cada caso existe atrito suficiente pa
Como indicado na Figura 10.46, um fio é enrolado diversas vezes em torno da periferia de um pequeno aro de raio 0,0800 m e massa igual a 0,180 kg. A extremidade livre do fio é puxada debaixo para cima
Um rolo de cortar grama com forma de uma casca cilíndrica de massa M é puxado horizontalmente com uma força constante horizontal F aplicada por um cabo ligado ao eixo. Sabendo que ele rola sem desliza