Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 3.Problemas - Ex. 30
Uma bola gira no sentido anti-horário em um círculo vertical na ponta de uma corda de de comprimento. Quando a bola passa a do ponto mais baixo em seu caminho para cima, sua aceleração total é . Para esse instante, (a) desenhe um diagrama vetorial mostrando as componentes de sua aceleração, (b) determine o módulo de sua aceleração radial e (c) determine a velocidade escalar e a velocidade da bola.
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer mais uma questãozinha aqui?
Vem comigo!
Letra a:
Ver figura abaixo:
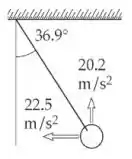
Passo 2
Letra b:
Os componentes das acelerações ao longo da corda juntas constituem a aceleração centrípeta:
Passo 3
Letra c:
Tangente ao círculo.
Resposta
- Ver figura
Exercícios de Livros Relacionados
16 .AF I G U R AQ 4.16 mostra um pêndulo na extremidade final do arco que ele descreve. a . Neste ponto, ω é positiva, negativa ou nula? Explique. b . Neste ponto, α é positiva, negativa ounula? Expli
14 . AF I G U R AQ 4.14 mostra três pontos sobre uma roda que está girando uniformemente. a . Ordene em seqüência, da maior para a menor, as velocidades angulares ω 1 , ω 2eω 3 destes pontos. Explique
A FIGURA Q4.15 mostra quatro rodas giro. Para cada uma, determine os sinais ( +o u- ) de ω e de α .
A roda de uma bicicleta bem lubrificada gira por um longo tempo antes de parar. Considere que uma roda dessas, girando inicialmente a 100r p m , leve 60s até parar. Se a aceleração angular for constan
Uma corda comprida é enrolada ao redor de um cilindro de 6,0c m de diâmetro, inicialmente em repouso, que é livre para girar em torno de um eixo. A corda, então, é puxada com uma aceleração constante