Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Questões Conceituais - Ex. 14
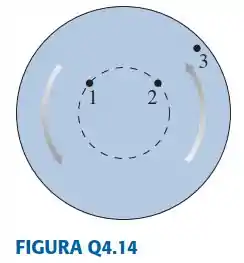
mostra três pontos sobre uma roda que está girando uniformemente.
Ordene em seqüência, da maior para a menor, as velocidades angulares destes pontos. Explique.
Ordene em seqüência, do maior para o menor, os módulos das velocidades desses pontos. Explique.
Passo 1
Ordene em seqüência, da maior para a menor, as velocidades angulares destes pontos. Explique.
A velocidade angular também é chamada de frequência angular, elas são a mesma coisa. E por vezes nos atrapalhamos por conta dos termos. Elas expressam a mesma coisa: o quanto algo se repete ao longo do tempo, mas um por meio de radianos e outra por meio de ciclos. Com essa relação aqui:
Dessa forma as velocidades angulares (frequência angular) serão as mesmas para qualquer ponto por que os repetições serão as mesmas ao longo do tempo, imagine a roda girando, independente do raio, das distancias entre o ponto e o centro... Uma volta da roda, será uma volta para todos os pontos.
Assim:
Passo 2
Ordene em seqüência, do maior para o menor, os módulos das velocidades desses pontos. Explique.
Já aqui as coisas serão diferentes, aqui estamos lidado com velocidade “bruta”, temos que olhar para o componente tangencial ao movimento, que é a velocidade, é esse vetor em violeta:
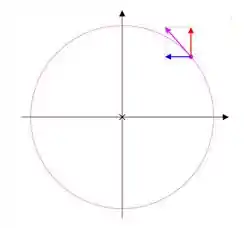
Como uma volta da roda, será uma volta para todos os pontos, (frequência é mesma), o ponto mais afastado do centro (), terá que “caminhar” mas rápido para poder acompanhar o ponto mais próximo do centro, visto que o perímetro da circunferência será maior para ele do que para os pontos e . Veja que e está no mesmo potencial, portando sua velocidade é a mesma.
Então a velocidade fica:
Nesse simulador gratuito vc pode perceber essas relações de forma mais intuitiva:
https://bit.ly/2yafexi