Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 12

Uma fita leve está enrolada em volta de um disco circular de massa m e raio r , que rola sem deslizar sobre um plano inclinado áspero de inclinação θ . A fita passa por uma roldana fixa de massa desprezível e está presa a um corpo suspenso de massa m ' (Fig.). Calcule (a) a aceleração a da massa m ' (b) a tensão T na fita.

Passo 1

Primeiro vamos fazer uma ilustração para entender melhor o que ta acontecendo.

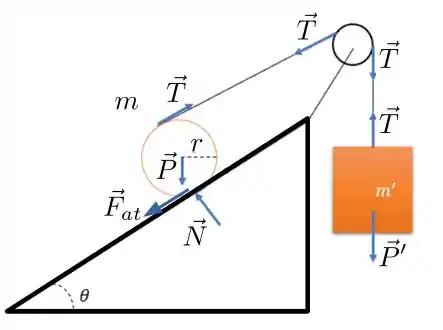
A F → a t aponta pra baixo por que o disco está sendo puxado pra cima pela corda e a tendência é que o ponto de contato da rampa com o disco seja empurrado para direita, então a força de atrito aponta na direção contrária, beleza?

Passo 2

Primeiro vamos olhar o bloco de massa m ' ! A segunda lei de Newton pra ele fica:

m ' g - T = m ' a  

T = m ' g - a   ( i )

Show!

Agora vamos analisar o disco. A segunda lei de Newton fica:

T - F a t - m g s e n θ = m a     i i

Passo 3

Agora vamos olhar pra rotação do disco. O torque é dado por

τ r e s = I α

Logo,

T r + F a t r = I α

r T + F a t = I α

Como temos um disco, I = 1 2 m r 2 . Além disso, α = a / r (por que o disco não escorrega):

r T + F a t = 1 2 m r 2 a r

Assim,

T + F a t = 1 2 m a   i i i

Show! Agora é “só” resolver esse sisteminha de equações :D

Passo 4

Vamos somar a primeira equação de i i com i i i .

2 T - m g s e n θ = 1 2 m a + m a

2 T - m g s e n θ = 3 2 m a

Agora vamos substituir a nossa equação i aqui

2 m ' g - a - m g s e n θ = 3 2 m a

4 m ' g - 4 m ' a - 2 m g s e n θ = 3 m a

Aí, vamos colocar tudo que tem a de um lado e tudo que g de outro

- 4 m ' a - 3 m a = 2 m g s e n θ - 4 m ' g

a 4 m ' + 3 m = g 4 m ' - 2 m s e n θ

a = g 4 m ' - 2 m s e n θ 4 m ' + 3 m

a = g m ' - m s e n θ 2 m ' + 3 4 m

Show! Agora só falta T !

Passo 5

Para calcular T , vamos substituir o a que acabamos de achar na equação i

T = m ' g - a = m ' g - g m ' - m s e n θ 2 m ' + 3 4 m = m ' g 1 - m ' - m s e n θ 2 m ' + 3 4 m

T = m ' g m ' + 3 4 m - m ' - m s e n θ 2 m ' + 3 4 m

T = m ' g m 3 4 + s e n θ 2 m ' + 3 4 m

Show! :D

Resposta

a)

a = g m ' - m s e n θ 2 m ' + 3 4 m

b)

T = m ' g m 3 4 + s e n θ 2 m ' + 3 4 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois corpos, de massas m 1 = 500 g e m 2 = 510 g , estão ligados por um fio de massa desprezível que passa por uma polia sem atrito. A polia é um isco uniforme de 50,0 g com um raio de 4,00 c m . O fi
O sistema da figura 9-57 é largado do repouso quando o bloco de 30 k g está 2,0 m acima da prateleira. A polia é um disco uniforme de 5,0 k g com um raio de 10 c m . Justo antes de o bloco de 30 k g a
Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro uniforme de massa m 1 e raio R gira sobre suportes sem atrito. Um fio sem massa, enrolado em torno do cilindro, está ligado a um bloco de massa m 2 , que está sobre um plano inclinado de θ
Um ioiô de 0.10 k g consiste em dois discos maciços, cada um de 10 c m de raio, ligados por uma haste sem massa de 1,0 c m de raio. Um fio está enrolado em volta da haste. Uma extremidade do fio é man