Na Fig. 10-38, dois blocos, de massas e , estão ligados por uma corda de massa desprezível que está enrolada na borda de um disco homogêneo de massa e raio . O disco pode girar sem atrito em torno de um eixo horizontal que passa pelo centro; a corda não desliza na borda do disco. O sistema é liberado a partir do repouso. Determine (a) o módulo da aceleração dos blocos, (b) a tensão da corda da esquerda e (c) a tensão da corda da direita.

Belezera pessoal, os blocos e a polia estão disposto como na figura a seguir:

Agora o bizu master pra facilitar nossas contas, é que podemos dividir a imagem em duas e analisar o sistema de maneira dividida.

Saca só, podemos traçar uma linha pontilhada imaginária desse jeito:

A malandragem da gente fazer isso, é que podemos olhar como se movimenta o bloco do lado esquerdo, de maneira separada do bloco que se movimenta do lado direito. Como a polia gira no sentido horário, vamos escolher ele como positivo, de maneira que a aceleração seja para cima como positivo para o bloco 1, e o sentido para baixo como positivo para o bloco 2

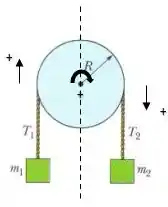
E como a corda é inextensível e desliza sem atrito, temos que a aceleração da corda é a mesma em qualquer ponto da corda. Então a aceleração do bloco e do bloco são iguais:

Agora aplicando a Segunda Lei de Newton no lado esquerdo, vamos ter que:

Já no lado direito, nós trocamos o sentido, de maneira que:

E se a gente ainda juntar com a equação para o torque:

Como a polia se trata de um disco homogêneo de momento inércia , com aceleração angular dada como , segue que:

Logo, vamos obter um sistema de equações, dado como: