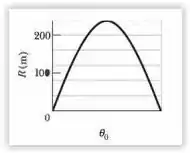
Uma bola é lançada a partir do solo com uma certa velocidade. A Fig. 4-45 mostra o alcance R em função ao ângulo de lançamento θ 0 . O tempo de percurso depende do valor de θ 0 ; seja t m á x á , o maior valor possível desse tempo. Qual é a menor velocidade que a bola possui durante o percurso se θ 0 é escolhido de tal forma que o tempo de percurso seja 0,500 t m á x á ?

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.6 - Ex. 52

Uma bola é lançada a partir do solo com uma certa velocidade. A Fig. 4-45 mostra o alcance em função ao ângulo de lançamento . O tempo de percurso depende do valor de ; seja , o maior valor possível desse tempo. Qual é a menor velocidade que a bola possui durante o percurso se é escolhido de tal forma que o tempo de percurso seja ?

Passo 1

Então galera, nós sabemos que a velocidade da bola vai ser a menor possível quando ela estiver na sua altura máxima, pois neste caso só haverá componente horizontal da velocidade.

Ou seja:

Nós sabemos também que o tempo de percurso pode ser calculado através da fórmula:

Sendo assim:

Isso quer dizer que na metade do tempo (), temos que , logo:

Portanto:

Passo 2

Agora precisamos achar a velocidade da componente horizontal , que coincide com a menor velocidade da bola durante o percurso. Temos que:

Agora temos que achar o valor de e para isso vamos usar o gráfico . O alcance da bola quando é . Sendo assim:

Logo:

Portanto a velocidade mínima será:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura representa a trajetória parabólica de um projétil indo de A até E . A resistência do ar é desprezível. Qual é a direção da aceleração no ponto (b)? (a) Para cima e para a direita, (b) para ba

A figura representa a trajetória parabólica de um projétil indo de A até E . A resistência do ar é desprezível. (a) Em quais pontos a rapidez é máxima? (b) Em quais pontos a rapidez é mínima? (c) Em q

Dois canhões estão apontados um para o outro, como mostrado na figura. Quando são disparadas, as bolas dos canhões vão seguir as trajetórias mostradas – P é o ponto onde as trajetórias se cruzam. Se q

Estime a distância a que você pode jogar uma bola se você a jogar (a) horizontalmente ao nível do solo, (b) Com θ = 45 ° acima da horizontal, enquanto está de pé no nível do solo, (c) horizontalmente

Você faz um arremesso, lançando uma bola de beisebol a 87 mi/h até a base, que está distante 18,4 m. Quanto a bola terá caído, por efeito da gravidade, ao chegar à base? (Ignore a resistência do ar.)