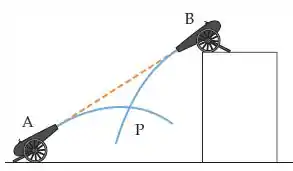
Dois canhões estão apontados um para o outro, como mostrado na figura. Quando são disparadas, as bolas dos canhões vão seguir as trajetórias mostradas – é o ponto onde as trajetórias se cruzam. Se queremos que as bolas colidam, deveríamos disparar o canhão primeiro, o canhão primeiro, ou os dois simultaneamente? Ignore os efeitos da resistência do ar.

Como os canhões estão apontados um para o outro, as componentes horizontais da velocidade inicial são iguais, e então as duas bolas vão atingir a coordenada horizontal do ponto ao mesmo tempo.

Agora vamos dar uma olhada na equação que descreve o movimento de uma das bolas:

aponta sempre na direção da linha pontilhada, e aponta na vertical para baixo (direção do vetor ).

Em outras palavras, te diz o quanto a bola foi “desviada” para baixo a partir da trajetória pontilhada.

Como é igual para os dois canhões, também podemos dizer que eles atingirão a coordenada vertical do ponto ao mesmo tempo.

Para resumir, se dispararmos os canhões ao mesmo tempo, as duas bolas já irão se colidir no ponto .