Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 104

Uma bola maciça e uniforme, com 20 g de massa e 5,0 c m de raio, é colocada sobre uma superfície horizontal. Uma força é aplicada sobre a bola, horizontalmente e 9,0 cm acima da superfície. Durante o impacto, a força cresce linearmente de 0,0 N até 40,0 k N , em 1,0 × 10 - 4 s , e depois ela decresce linearmente até 0,0 N em 1,0 × 10 - 4 s . (a) Qual é a rapidez da bola imediatamente após o impacto? (b) Qual é a rapidez angular da bola após o impacto? (c) Qual é a rapidez da bola quando ela começa a rolar sem deslizar? (d) Qual a distância percorrida pela bola sobre a superfície antes de começar a rolar sem deslizar? Suponha μ c = 0,50 .

Passo 1

Então, meu favorecido, o que a gente tem que perceber aqui é que essa força vai dar um impulso na bola, de forma que vai fazer variar sua quantidade de movimento. Durante a aplicação da força a bola vai estar acelerando, que é a situação das letras (a) e (b), e depois que a força para de atuar, a bola vai girar sem deslizar, e aí podemos usar aquela relação da velocidade escalar com velocidade angular v = ω r . Vai com calma que essa questão é ENORME.

Passo 2

Para as situações (a) e (b) o diagrama de corpo livre fica assim:

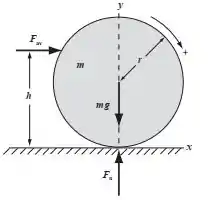
  1. O impulso da força F vai ser o responsável pela aceleração da bola. Vamos usar o teorema impulso-momento pra ver até qual velocidade a bola vai.

    2. F m é d i a Δ t = Δ p = m v 0

    Como vamos achar a força média? É fácil! Em uma situação em que a variável cresce linearmente, o seu médio é realmente o valor do meio. Nesse caso, como ela cresce de 0,0 N até 40,0 k N , a força média será:

    F m é d i a = 0,0 k N + 40,0 k N 2 = 20,0 k N

    Então, substituindo na fórmula, sem cair na casca de banana das unidades:

    ( 20,0 × 10 3 N ) × 2 × 10 - 4 s = 0,020 k g × v 0

    v 0 = 200 m s

    Passo 3

  2. Vamos analisar agora a dinâmica da rotação do corpo:

    3. ∑ τ = I c m α

    F m é d i a h - r = I c m ω 0 Δ t

    ω 0 = F m h - r Δ t I c m

    ω 0 = F m h - r Δ t 2 5 m r 2

    Como já vimos no outro ítem, F m Δ t = m v 0 → Δ t = m v 0 F m   .

    ω 0 = F m h - r m v 0 F m 2 5 m r 2 = 5 v 0 h - r 2 r 2

    Substituindo os valores numéricos:

    ω 0 = 5 × 200 × 0.090 - 0.050 2 0.050 2

    ω 0 = 8 × 10 3   r a d / s

    Passo 4

    Agora vamos ficar com a seguinte situação para os itens (c) e (d):

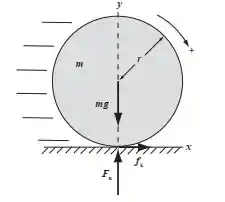
  3. Para acharmos a direção da força de atrito, vamos comparar a velocidade angular depois do impacto é maior, menor ou igual à velocidade angular da condição de rolamento sem deslizamento, que vale v 0 r = 200 0.05 = 4 × 10 3 r a d / s .

    4. Vamos olhar agora para dinâmica da situação:

    No eixo x :

    F x = f a t = m a c m

    No eixo y :

    F y = N - m g = 0 → f a t = μ m g = m a c m

    a c m = μ g

    Para a rotação:

    ∑ τ = - f a t r = I α

    α = - f a t r I

    α = - μ m g r 2 5 m r 2

    α = - 5 μ g 2 r

    Olhamos para o movimento agora:

    ω = ω 0 + α t = ω 0 - 5 μ g t 2 r

    Se a bola rola sem deslizar, v = ω r .

    v c m = r ω 0 - 5 μ g t 2 r = r ω 0 - 5 μ g t 2

    Mas v = v 0 + a t !

    r ω 0 - 5 μ g t 2 = v 0 + μ g t

    t = 2 r ω 0 - v 0 7 μ g

    Substituindo valores, vamos achar:

    t = 2 0.05 × 8 × 10 3 - 2 × 10 2 7 × 0.5 × 9.81

    t = 11.65 s

    E assim:

    v = 2 × 10 2 + 0.5 × 9.81 × 11.65

    v = 2.57 × 10 2 m / s

    Passo 5

  4. A distância que a bola vai viajar pode ser calculada pela equação principal do movimento:

Δ x = v 0 t + a t 2 2

Δ x = 2 × 10 2 × 11.65 + 0,50 × 9.81 × 11.65 2 2

Δ x = 3000 m

Resposta

  1. v 0 = 200 m s
  2. ω 0 = 8 × 10 3   r a d / s
  3. v = 2.57 × 10 2 m / s
  4. Δ x = 3000 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de boliche, de raio R , começa a rolar sobre a pista com uma rapidez angular ω 0 = 3 v 0 / R , onde v 0 é sua rapidez inicial. O coeficiente de atrito cinético é μ c . (a) Qual é a rapidez da
Uma bola de gude de massa M e raio R desce rolando, sem deslizar, pelo trilho da esquerda, a partir de uma altura h 1 , como mostrado na figura. Depois, ela sobre o trilho sem atrito da direita, até a
Em uma competição, você percebe que a sua bola de boliche volta rolando para você sempre sem deslizar, na parte plana da pista. Quando ela chega à rampa que a trará de volta para você, ela está a 3,70
Um aro uniforme de 1,5 k g , com 65 c m de raio, tem sua circunferência envolvida por um cordão e é colocado sobre uma mesa horizontal sem atrito. A extremidade livre do cordão é puxada com uma força