Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 107

Uma bola de boliche, de raio R , começa a rolar sobre a pista com uma rapidez angular ω 0 = 3 v 0 / R , onde v 0 é sua rapidez inicial. O coeficiente de atrito cinético é μ c . (a) Qual é a rapidez da bola assim que ela começa a rolar sem deslizar? (b) Qual é o tempo transcorrido durante o deslizamento até que a bola começa a rolar sem deslizar? (c) Qual é a distância percorrida pela bola durante o deslizamento até começar a rolar sem deslizar?

Passo 1

Bora lá, galera, aqui a gente vai resolver as letras (a) e (b) juntas. Eu fiz aqui o diagrama de corpo livre da bola de boliche.

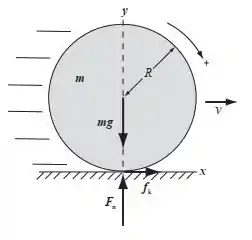
Primeiro vamos aplicar a segunda lei de Newton para a bola.

No eixo y :

N = m g → F a t = μ c m g

No eixo x :

m a = F a t = μ c m g → a = μ c g

Para a rotação:

∑ τ = - F a t R = I α

O sinal de menos é porque o atrito faz girar no sentido anti-horário, e o eixo positivo que escolhi foi rodar no sentido horário.

α = - F a t R I = - m μ c g R 2 5 m R 2

α = - 5 μ c g 2 R

Passo 2

Se temos a aceleração angular e a tangencial, podemos escrever a equação do movimento da bola:

v = v 0 + a t = v 0 + μ c g t   ( * )

ω = ω 0 + α t = ω 0 - 5 μ c g t 2 R

Ele disse enunciado que a bola rola sem deslizar. Isso já chama o que??? Isso aí, v = ω R . Do enunciado, a gente sabe que ω 0 = 3 v 0 R .

v 0 + μ c g t = R ω 0 - 5 μ c g t 2 R = R 3 v 0 R - 5 μ c g t 2 R

v 0 + μ c g t = 3 v 0 - 5 μ c g t 2

7 μ c g t 2 = 2 v 0

t = 4 v 0 7 μ c g

Substituindo na equação marcada com ( * ) :

v = v 0 + μ c g 4 v 0 7 μ c g

v = 11 v 0 7

Passo 3

c) A distância alcançada pela bola vai ser igual a:

Δ x = v m t

Como podemos achar essa velocidade média? É simples: como a velocidade varia linearmente, a velocidade média vai ser igual à média das velocidades inicial e final.

v m = v 0 + v 2 = v 0 + 11 v 0 7 2 = 9 v 0 7

Então é só substituir!

Δ x = 9 v 0 7 4 v 0 7 μ c g

Δ x = 36 v 0 2 49 μ c g

Resposta

  1. v = 11 v 0 7
  2. t = 4 v 0 7 μ c g
  3. Δ x = 36 v 0 2 49 μ c g
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro maciço e uniforme, de madeira, rola descendo um plano inclinado de um ângulo θ , sem deslizar. O coeficiente de atrito estático é μ . Determine (a) a aceleração do centro de massa do cilin
Uma esfera maciça e uniforme rola descendo um plano inclinado, sem deslizar. Se a aceleração linear do centro de massa da esfera é 0,20 g , qual é o ângulo de inclinação do plano com a horizontal?
Uma bola de basquete rola descendo um plano inclinado de um ângulo θ , sem deslizar. O coeficiente de atrito estático é μ . Trate a bola como uma casca esférica fina. Determine (a) a aceleração do cen
Um cilindro maciço e uniforme, de massa M e raio R , é colocado sobre uma barra de massa m , que, por sua vez, está sobre uma mesa horizontal sem atrito (figura 9-65). Se uma força F → é aplicada sobr
Uma bola de bilhar, inicialmente em repouso, recebe uma forte tacada. A força é horizontal e aplicada a uma distância 2 R 3 abaixo da linha diametral, como mostra a figura. A rapidez da bola imediatam