Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 111

Uma barra fina uniforme de 0,25 k g , de 80 c m de comprimento, pode girar livremente em torno de um eixo fixo horizontal que passa, perpendicularmente, por uma de suas extremidades. Ela é largada da horizontal. Imediatamente após a largada, qual é (a) a aceleração do centro da barra e (b) a aceleração da extremidade livre da barra? (c) Qual é a rapidez do centro de massa da barra quando ela está (momentaneamente) na vertical?

Passo 1

Bora lá, galerinha, uma questão um pouco diferente do que viemos fazendo até então. Nessa, uma barra gira em torno de um eixo, e queremos saber a aceleração em alguns momentos. Aqui eu fiz uma representação da barra:

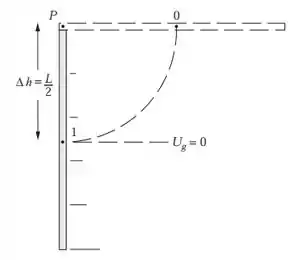
Nós vamos ter que lembrar daquela relação a = α r , que relaciona a aceleração tangencial e a angular!

Passo 2

  1. Para o ponto médio da barra:

    2. a = L 2 α

    Mas da segunda lei de Newton nós sabemos que:

    τ = I α → α = τ I

    α = M g L 2 M L 2 3

    α = 3 g 2 L = 3 × 9.81 2 × 0.80 = 18.4 r a d / s 2

    Então,

    a = L 2 × 3 g 2 L = 3 g 4

    a = 3 × 9.81 4

    a = 7,4 m / s 2

    Passo 3

  2. Agora, para a ponta da barra:

    3. a p o n t a = L α

    a p o n t a = 0.8 × 18.4

    a p o n t a = 15 m / s 2

    Passo 4

  3. Como sabemos, na rotação, v = ω r . Como o centro de massa da barra está a uma distância igual à metade da barra do ponto fixo:

v = ω L 2

No começo tinha energia potencial gravitacional, que vai se converter em energia cinética rotacional. Conservando a energia:

m g h = I ω 2 2

m g L 2 = m L 2 3 ω 2 2

ω = 3 g L

Então,

v = 3 g L L 2

v = 3 g L 2

Substituindo valores:

v = 3 × 9.81 × 0.80 2

v = 2.4 m / s

Resposta

  1. a = 7,4 m / s 2
  2. a p o n t a = 15 m / s 2
  3. v = 2.4 m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um torque resultante constante atua sobre um carrossel desde a partida, até que ele atinja a rapidez de operação. Durante este tempo, a energia cinética do carrossel (a) é constante, (b) cresce linear
A orientação da velocidade angular de um corpo é, necessariamente, a mesma do torque resultante sobre ele? Explique. Se o torque resultante e a velocidade angular têm sentidos opostos, o que isto lhe
Uma forma de identificar se um ovo está cozido ou não sem quebrá-lo, é colocar o ovo sobre uma superfície horizontal rígida e tentar girá-lo. Um ovo cozido vai girar com facilidade, contrariamente ao
Verdadeiro ou falso: Se o torque resultante sobre um objeto em rotação é zero, a velocidade angular do objeto não pode mudar. Se sua resposta é “falso”, dê um exemplo de tal situação.
Um bloco deslizando sobre uma mesa sem atrito está amarrado a um fio que passa por um pequeno furo através da mesa. Inicialmente, o bloco está deslizando com rapidez v 0 em um círculo de raio r 0 . Um