Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 119

Em uma competição, você percebe que a sua bola de boliche volta rolando para você sempre sem deslizar, na parte plana da pista. Quando ela chega à rampa que a trará de volta para você, ela está a 3,70 m / s . O comprimento da rampa é 2,50 m . O raio da bola de boliche é 11,5 c m . (a) Qual é a rapidez angular da bola, imediatamente antes de chegar à rampa? (b) Se a rapidez com que a bola emerge do topo da rampa é 0,40 m / s , qual é o ângulo (suposto constante) que a rampa forma com a horizontal? (c) Qual é a magnitude da aceleração angular da bola enquanto está na rampa?

Passo 1

Aqui a figura mostra a bola desacelerando ao longo da rampa. Essa é moleza, vamos usar conservação da energia para a situação de cima e de baixo da rampa e acabou!

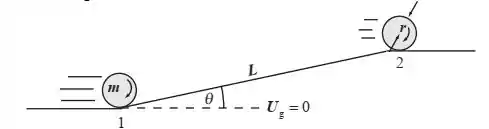
  1. Como a bola rola sem deslizar, podemos dizer que v = ω r .

    2. ω = v r = 3.70 0.115

    ω = 32.2 r a d s

    Passo 2

  2. Inicialmente a bola tinha energia cinética, e depois parte dessa energia cinética vira potencial gravitacional. Da figura, a gente vê que o bloco sobe uma altura h = L s e n θ .

    3. m v 1 2 2 + I ω 1 2 2 = m g L s e n θ + m v 2 2 2 + I ω 2 2 2

    m v 1 2 2 + 2 5 m r 2 ω 1 2 2 = m g L s e n θ + m v 2 2 2 + 2 5 m r 2 ω 2 2 2

    m v 1 2 2 + 2 5 m v 1 2 2 = m g L s e n θ + m v 2 2 2 + 2 5 m v 2 2 2

    7 10 v 1 2 = g L s e n θ + 7 10 v 2 2

    s e n θ = 7 v 1 2 - v 2 2 10 g L

    θ = a r c s e n 7 v 1 2 - v 2 2 10 g L

    Substituindo valores:

    θ = a r c s e n 7 3.70 2 - 0.40 2 10 9.81 2.5

    θ = 23 °

    Passo 3

  3. A aceleração angular vem da relação a = α r .

Pela equação de Torricelli,

v 2 2 = v 1 2 + 2 a L

a = v 2 2 - v 1 2 2 L

Logo,

α = v 2 2 - v 1 2 2 L r

Substituindo valores:

α = 0.40 2 - 3.70 2 2 0.115 2.5

α = 24   r a d / s 2

Resposta

  1. ω = 32.2 r a d s
  2. θ = 23 °
  3. α = 24 r a d s 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pedras que rolam. Uma pedra esférica, uniforme e maciça parte do repouso e rola para baixo de uma colina de 50,0m de altura, como indica a Figura 10.60 . A metade superior da colina é áspera o suficie
Em uma experiência de laboratório você faz uma bola homogênea rolar para baixo de um rilho curvo. A bola parte do repouso e rola sem deslizar. Enquanto está sobre o trilho, a bola desce uma distância
Em uma catapulta de mola, a constante da mola é igual a 400 N/m e a mola sofre uma compressão de 0,15 m. Quando ela é disparada, 80% da energia potencial elástica armazenada na mola é convertida em en
Quando uma roda rola ao longo de uma superfície horizontal com velocidade constante, as coordenadas de um ponto na periferia da roda são x t = R [ 2 π t T - sin ⁡ 2 π t T ] e y t = R [ 1 - cos ⁡ ( 2 π
Um ioiô de massa M , raio interno r , raio externo R e momento de inércia I C M em relação ao seu centro e massa, é puxado pelo fio enrolado em seu eixo central, de forma a rolar sem deslizamento sobr