Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.Problemas - Ex. 115
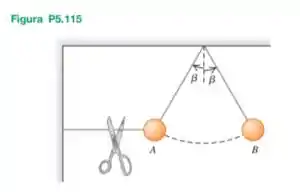
Uma bola é mantida em repouso na posição A indicada na Figura P5.115 por meio de dois fios leves. O fio horizontal é cortado e a bola começa a oscilar como um pêndulo. O ponto B é o mais afastado do lado direito da trajetória das oscilações. Qual é razão entre a tensão do fio na posição B e a tensão do fio na posição A antes de o fio horizontal ser cortado?
Passo 1
Fala galerinha, beleza?
O primeiro passo para resolver esse problema é desenhar as forças que agem sobre a bolinha em cada posição:
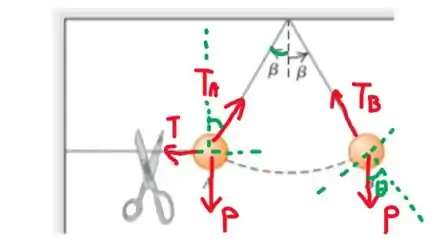
Na posição A, temos uma situação de equilíbrio estático, de modo que
Logo,
Passo 2
Na situação B, temos que considerar a resultante centrípeta:
Como a bola está instantaneamente em repouso no ponto B, temos que
Com isso, a razão entre as tensões é
Resposta
Exercícios de Livros Relacionados
Suponha que o coeficiente de atrito estático entre a estrada e os pneus de um carro é 0,60 e não há sustentação negativa. Que velocidade deixa o carro na iminência de derrapar quando faz uma curva não
Um carrinho de brinquedo com massa m trafega em velocidade constante no interior de uma pista que é um círculo vertical com raio de 5,00m (Figura E5.45). Se a força normal exercida pela pista sobre o
Uma estrada na direção leste passa por uma pequena colina. Você dirige um carro com massa m a uma velocidade constante v sobre o topo da colina, onde a forma da rodovia é bem próxima do arco de um cír
João senta-se cadeira de uma roda-gigante que está girando a uma velocidade constante de 0,100 rotações/segundo. Quando João passa pelo ponto mais alto de sua trajetória circular, a força para cima qu