Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.4 - Ex. 47
Um carrinho de brinquedo com massa trafega em velocidade constante no interior de uma pista que é um círculo vertical com raio de (Figura E5.45). Se a força normal exercida pela pista sobre o carro quando ele está na base da pista (ponto A) é igual a , quanto tempo é necessário para que o carro complete uma volta pela pista?
Passo 1
Fala pessoal, bora resolver um probleminha de movimento circular?
Esse exercício é bem parecido com o anterior, então começamos desenhando as forças:
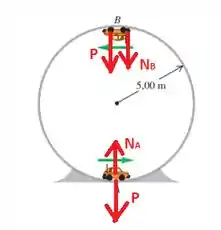
Repare que, no ponto A, a força normal aponta para dentro do círculo e o peso para fora. Já no ponto B ambos apontam para dentro!
Com isso podemos usar a relação:
No ponto A encontramos:
Já no ponto B:
Passo 2
Vamos focar nossa atenção no ponto A (base da pista) e lembrar que
Assim,
O enunciado deu que e você deve saber que , de modo que
Usando e , temos que
Passo 3
O exercício quer que achemos o período:
Assim,
Logo,