Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 89

Uma bola de 2,0 k g , movendo-se a 10 m / s , sofre uma colisão oblíqua com uma bola de 3,0 k g que está inicialmente em repouso. Após a colisão, a bola de 2,0 k g é defletida de um ângulo de 30 ° em relação à sua orientação original de movimento e a bola de 3,0 k g está se movendo a 4,0 m / s . Determine a rapidez da bola de 2,0 k g e a orientação da bola de 3,0 k g , após a colisão.

Passo 1

A colisão vai ter essa cara aí. Precisamos encontrar a velocidade final da bola 2 e o ângulo que a bola 3 faz com a horizontal.

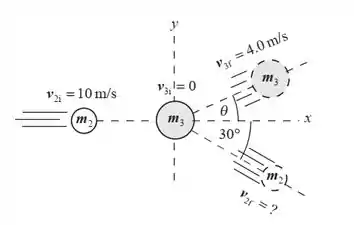
Pra isso é só o usar o de sempre: quantidade de movimento!

Passo 2

No eixo x :

m 2 v 2 i = m 2 v 2 f c o s 30 ° + m 3 v 3 f c o θ

2 × 10 = 2 v 2 f 3 2 + 3 × 4 c o s θ

v 2 f 3 + 12 c o s θ = 20

c o s θ = 20 - 3 v 2 f 12

No eixo y :

m 3 v 3 f s e n θ = m 2 v 2 f s e n 30 °

3 × 4 s e n θ = 2 v 2 f × 1 2

12 s e n θ = v 2 f

s e n θ = v 2 f 12

Passo 3

Usando a relação fundamental s e n 2 θ + cos 2 ⁡ θ = 1 , obtemos:

v 2 f 12 2 + 20 - 3 v 2 f 12 2 = 1

v 2 f 2 + 20 - 3 v 2 f 2 = 144

v 2 f 2 + 400 - 40 3 v 2 f + 3 v 2 f 2 = 144

4 v 2 f 2 - 40 3 v 2 f + 256 = 0

v 2 f 2 - 10 3 v 2 f + 64 = 0

Resolvendo a equação vamos encontrar duas raízes: v 2 f = 5.344 m / s   e v 2 f = 11.977 m / s .

Mas a velocidade inicial da massa era 10 m / s . A segunda raiz seria equivalente a aumentar a energia do sistema, o que é impossível. Logo : v 2 f = 5.344 m / s .

Passo 4

Agora é só substituir na equação lá em cima:

s e n θ = v 2 f 12 = 5.344 12

θ = 26 °

Resposta

θ = 26 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A partícula 1 , com massa de 200g e uma velociade de 3,00m / s , sofre uma colisão unidimensional com uma partícula 2 , com uma massa de 400g , inicialmente em repouso. Qual é o módulo do impulso sobr
Um núcleo atômico em repouso na origem de um sistema de coordenadas x y se transforma em três partículas. A partícula 1 , de massa 16,7 × 10 - 27k g , se afasta da origem com uma velocidade de ( 6,00
Um vagão de trem pesando 280k N e viajando a 1,52m / s alcança outro pesando 210k N e viajando a 0,914m / s no mesmo sentido. Se os vagões permanecem juntos após a colisão, determine (a) a velociade d
Um próton desloca-se para a direita a 2,0 × 10 7m / s . Ele sofre uma colisão frontal e perfeitamente elástica com um átomo de carbono. A massa deste átomo é doze vezes maior que a do próton. Qual é a
Uma bolinha de 50g , movendo-se a 2,0m / s , colide com outra bolinha de 20 g que está parada. Qual é o módulo da velocidade de cada bolinha imediatamente após a colisão?