Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 50
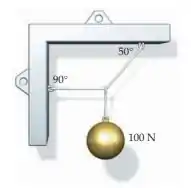
Uma bola pesando 100 N é mostrada suspensa por um sistema de cordas (Figura 4-39). Quais são as tensões nas três cordas?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A bolinha pesa . Aí uma corda segura ela e outras duas cordas seguram essa primeira corda.
Queremos a força que cada corda deve suportar para que essa bolinha fique paradinha onde está, ou seja, fique em equilíbrio.
Uma coisa que a gente pode ver antes de fazer continhas é que a corda de baixo é a única que liga a bola às outras duas cordas. Ela está sendo suportada pelas cordas de cima, mas ela segura sozinha a bola.
Se a bola tem peso e a corda de baixo suporta ela sozinha, o quanto a corda tem que suportar? O peso da bola! Então achamos nossa primeira força
Aí para achar as outras, vamos fazer um diagrama de corpo livre desse ponto onde as cordas se encontram:
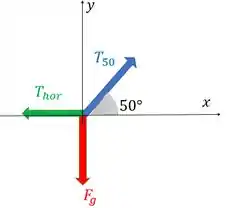
Esse ângulo foi achado pela geometria do problema mesmo.
Como estamos paradinhos em equilíbrio, a aceleração nas duas direções e é nula. Então, a partir desse diagrama, podemos usar a segunda lei de Newton para cada direção e achar e .
Bora lá!
Passo 2
Para a direção vertical, a segunda lei de Newton fica:
Vimos que :
Esse somatório é a soma das componentes de todas as forças que temos em respeitando a orientação delas. Nessa direção a gente tem a força peso para baixo, que vai entrar no somatório com sinal negativo por estar para baixo.
Temos também as componentes das tensões em , dadas por:
Usamos seno porque o ângulo de é oposto ao eixo , e a componente de é nula porque ela está coincidindo com o eixo .
Voltando para a segunda lei de Newton e escrevendo a soma dessas componentes, ficamos com:
Passo 3
Vamos fazer o mesmo para o eixo . As componentes das forças nele são:
A tensão está no eixo apontando para o sentido negativo, por isso sua componente é ela mesma com sinal de menos. Já está em , por isso sua componente em é zero. E usamos cosseno na componente de porque está colado no eixo .
O somatório dessas componentes em fica:
Substituindo isso na segunda lei de Newton para a direção que tem essa carinha:
E lembrando que porque estamos no equilíbrio:
Logo
Mas a gente sabe quem é :