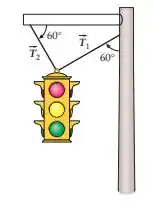
Um sinal luminoso de trânsito, de 35,0 kg, é mantido suspenso por dois fios, como na Figura 4-36. (a) Desenhe o diagrama de corpo livre para o sinal e utilize-o para responder qualitativamente à seguinte questão: A tensão no fio 2 é maior que a tensão no fio 1? (b) Confirme sua resposta aplicando as leis de Newton e calculando suas tensões.

b) Ele quer que a gente use a segunda lei de newton para descobrir o valor de e de . Então vamos aplicar essa lei para cada direção que a gente tem e .

Para a direção vamos ter:

Como a gente sinal de trânsito está parado, temos . Já o somatório de forças nessa direção é o somatório das componentes das forças nessa direção. As componentes de e em são:

A gente usa cosseno porque o ângulo que dá orientação dessas forças está colado em . E é negativo porque ele aponta para o sentido negativo de .

Nosso somatório em fica:

Substituindo isso na lei de Newton e lembrando que :

Agora vamos olhar para direção . Nessa direção a gente tem a força peso para baixo, que vai entrar no somatório com sinal negativo por estar para baixo, e temos também as componentes das tensões em , dadas por:

Usamos seno porque os ângulos são opostos ao eixo . O somatório de forças nessa direção fica:

Com isso, a gente consegue aplicar a segunda lei de Newton para essa direção:

Temos porque não há movimento nessa direção. Substituindo isso e nosso somatório:

Lembrando que a força peso tem a expressão , onde é a massa do sinal e a aceleração da gravidade, e substituindo na nossa equação:

Substituindo a expressão que a gente achou para lá no passo 2:

Isolando a tensão e substituindo os dados que a gente tem :

Voltando a usar a equação do passo 2 para descobrir :

Vemos que de fato é maior que 😊