Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 39
Em um piso, um homem passa o esfregão que, por causa do movimento, sofre dois deslocamentos. O primeiro tem módulo de e forma um ângulo de com um eixo positivo. O deslocamento resultante tem módulo de e direção de um ângulo de em relação ao eixo positivo. Encontre o módulo e a direção do segundo deslocamento.
Passo 1
Eai pessoal. Vamos resolver mais uma questão?
Nesta vamos ter que fazer uma interpretação de texto e desenhar. Mas por que desenhar? Pessoal fica mais fácil de entender onde estão localizados os vetores e como podemos resolver.
Vamos Começar!
Nesta questão ele já fala sobre a localização de dois vetores, o vetor 1 e o vetor resultante, vamos colocar em um plano cartesiano.
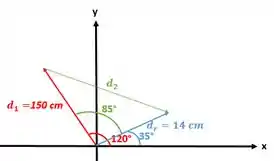
O nosso objetivo é encontrarmos o a direção do segundo deslocamento e seu módulo. A direção já foi identificado através do desenho (Viu como desenho é importante ;) ). E o módulo podemos encontrar através da Lei dos cossenos.
Passo 2
Temos que ter cuidado nesta parte, isso porque nós temos os vetores resultante (a) e um cateto (b), logo precisamos encontrar o outro cateto (c).
Resolvendo esta equação por Baskara, temos.
Passo 3
Agora temos que voltar a analisar os vetores. Vamos lembrar que os deslocamentos foram feitos em um movimento simultâneo, não foram realizados a partir da origem como mostrados na imagem acima. A imagem acima, só serviu para entendermos como os vetores são colocados em um plano cartesiano e como poderíamos resolver.
Vamos ver como realmente foi o movimento!
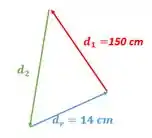
Podemos perceber que o deslocamento 2 está para baixo, ou seja possui orientação negativa para y e para x. sendo assim o deslocamento será 284,2 cm.
Resposta
O módulo do segundo vetor é 284,2 e está para baixo da direita para esquerda.