Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 11
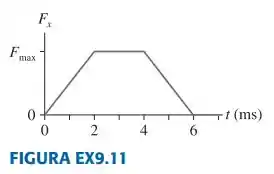
Uma bola de tênis de 60 g com velocidade inicial de 32 m/s colide com uma parede e ricocheteia com o mesmo valor de velocidade. A FIGURA EX9.11 representa a força da parede sobre a bola durante a colisão. Qual é o valor de , o máximo valor da força de contato durante a colisão?
Passo 1
O teorema impulso-momentum correlaciona a força aplicada por um determinado tempo (impulso) em um corpo com a variação da sua velocidade, que está ligada a seu momentum.
A seguinte equação descreve o teorema:
Onde e são respectivamente o impulso e o momentum do corpo. Essa equação pode ser reescrita em termo de escalares, assim:
Onde , t, e e são, respectivamente, a força aplicada, o tempo de ação da força, a massa do corpo e as velocidades inicial e final do corpo no intervalo de tempo avaliado.
Passo 2
Aqui o objetivo vai ser calcular a força . Já sabemos de exercícios anteriores que o impulso, em um gráfico equivale numericamente à área formada entre o eixo e a curva que representa a força.
Pra calcular o impulso, calculamos a área do trapézio. Ela é dada pela seguinte expressão:
Onde , e são as bases e a altura do trapézio, respectivamente. Nesse caso, a altura equivale à força máxima . Observando o gráfico, pra essa área, temos:
Repara que convertemos milissegundos pra segundos, pra que tudo fique no sistema internacional de unidades.
Passo 3
Agora, vamos avaliar as velocidades inicial e final da bola.
A velocidade é um vetor, certo? E quando escrevemos o vetor na forma de um escalar, como fizemos pra chegar na expressão lá de cima do Passo 1, temos que levar em conta sempre o sinal do escalar.
Quando a bola seguia em direção à parede, por convenção, a velocidade era positiva. No que ela ricocheteia, volta no sentido oposto, então tem velocidade negativa.
O módulo da velocidade é de 32 m/s. Assim, e , já que está no sentido oposto do convencionado positivo.
Temos finalmente pra expressão, o seguinte:
Onde , já convertido pro sistema internacional de unidades.
Passo 4
Agora, podemos igualar as duas partes da expressão completa que já temos pra chegarmos a um valor pra . Assim:
Teremos: