Uma caixa de encontra-se em repouso na base de uma rampa com de extensão, inclinada a acima da horizontal. O coeficiente de atrito cinético é , e o coeficiente de atrito estático é . Que força constante , aplicada paralelamente à superfície da rampa, é necessária para empurra a caixa até o topo da rampa em um tempo de ?

Fala pessoal, bora resolver um probleminha de plano inclinado?

Você já deve saber que a componente puxa a caixa para baixo no plano inclinado. Além disso, como a caixa vai subir a rampa no problema, o atrito (contrário ao movimento) deve apontar no mesmo sentido que a componente do peso. Com isso, a segunda lei de Newton fica:

Um diagrama de forças com a decomposição do peso é mostrado na figura:

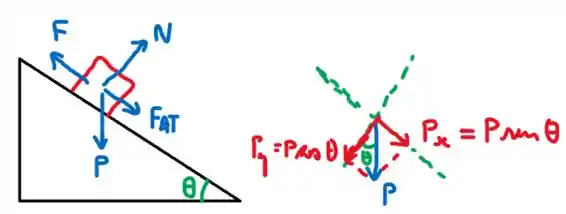
Vale lembrar que

Assim,

Logo,