Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 92

Dois blocos de massas 4,0   k g e 8,0   k g   estão ligados por um fio e deslizam 30 ° para baixo de um plano inclinado (Figura 5.74 ). O coeficiente de atrito cinético entre o bloco de 4,0   k g e o plano é igual a 0,25 ; e o coeficiente entre o bloco de 8,0   k g e o plano é igual a 0,35.

a) Qual é a aceleração de cada bloco?

b) Qual é a tensão na corda?

c) O que ocorreria se as posições dos blocos fossem invertidas, isto é, se o bloco de 4,0   k g estivesse acima do bloco de 8,0   k g ?

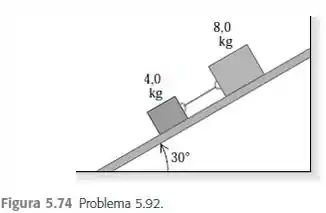
Passo 1

Opa, bora resolver esse problema! Temos a seguinte situação:

O enunciado também fala nos dá os coeficientes de atrito cinético:

E n t r e   o   b l o c o   d e   4,0   k g   e   o   p l a n o → μ 1 = 0,25

E n t r e   o   b l o c o   d e   8 , 0   k g   e   o   p l a n o → μ 2 = 0,3 5

A letra (a) nos pergunta a aceleração de cada broco!

Vamos entender o que está havendo. Temos que o bloco maior (maior massa) tem um atrito maior com a rampa, em relação ao atrito que o bloco menor (menor massa) tem com a rampa.

Daí podemos considerar que o bloco maior não vai deslizar mais rápido. Mas a aceleração de cada bloco vai ser igual, com o bloco menor puxando o bloco maior. E podemos considerar que o cabo entre eles está tracionado e os blocos se movem juntos. Assim, eles formam um sistema de aceleração única.

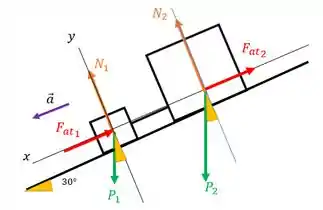
Para a gente achar essa aceleração, podemos aplicar a segunda lei de newton no sistema todo. Vamos avaliar quais forças estão externas a esse sistema:

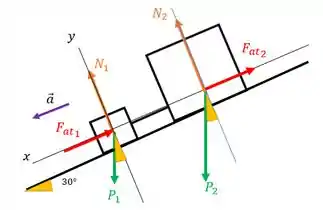
Temos a força peso de cada bloco (vertical para baixo), as forças normais (perpendiculares a superfície de contato) e as forças de atrito na direção contrária ao movimento. Sendo que as forças de atrito são dadas por

F a t = N μ

Passo 2

Vamos então aplicar a segunda lei de newton ao eixo x da figura, onde temos a nossa aceleração. Lembrando que aqui vamos olhar para o sistema constituído dos dois blocos

Temos que

∑ F x = m t a

Essa massa total é a massa dos dois blocos juntas m t = m 1 + m 2 . Aí substituindo as forças

P 1   s e n   30 ° - F a t 1 + P 2   s e n   30 ° - F a t 2 = m t a

Substituindo nossos dados:

m 1 g   s e n   30 ° - N 1 μ 1 + m 2 g   s e n   30 ° - N 2 μ 2 = m 1 + m 2 a

m 1 g   s e n   30 ° - P 1 cos ⁡ 30 ° μ 1 + m 2 g   s e n   30 ° - P 2 cos ⁡ 30 ° μ 2 = m 1 + m 2 a

m 1 g   s e n   30 ° - m 1 g cos ⁡ 30 ° μ 1 + m 2 g   s e n   30 ° - m 2 g cos ⁡ 30 ° μ 2 = m 1 + m 2 a

Sabendo que

m 1 = 4 k g

m 2 = 8 k g

μ 1 = 0,25

μ 2 = 0,35

Agora é só substituir tudo para descobrir o valor da aceleração:

a = 2,21 m / s 2

Passo 3

b) A corda está tensionada. Nosso DCL de cada bloco fica:

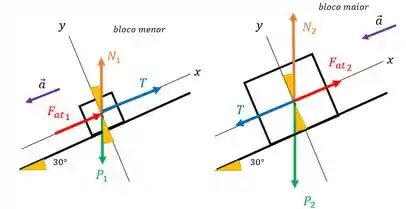
Agora isolando um dos blocos podemos determinar a tensão na corda. Vou escolher o bloco de cima. Poderia ser o outro, encontraria o mesmo valor! Como exercício eu recomendo você tentar =)

Aplicando a segunda lei para o bloco de 8 k g :

∑ F x = m a

P 2 + T - F a t 2 = m 2 a

m 2   g   s e n 30 + T - μ 2   m 2   g   c o s 30 = m 2   a

8 × 9,8 s e n 30 + T - 0,35 × 8 × 9,8   c o s 30 = 8 × 2,21

T = 17,7 + 23,76 - 39,2

T = 2,26 N

Passo 4

c) Temos que o bloco menor tem menor coeficiente de atrito e menor massa, então a força de atrito sobre ele é menor. E o bloco maior tem maior força de atrito.

Se as posições dos blocos fossem invertidas o bloco com menor atrito estaria acima e o com maior atrito estaria abaixo. Isso nos faz pensar que o bloco maior ia deslizar menos que o bloco menor, ou nem iria deslizar. Enquanto o bloco menor ia deslizar mais.

Com isso, a corda ficaria com folga, pois o bloco maior se moveria com uma aceleração menor. O bloco de 4 k g iria colidir com o bloco de 8 k g .

Resposta

a )   a = 2,21 m / s 2

b )   T = 2,26 N

c )   corda ficaria com folga, e haveria colisão entre blocos

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força horizontal F → de 12N empurra um bloco de 5,0N de peso contra uma parede vertical (Fig. 6-26). O coeficiente de atrito estático entre a parede e o bloco é 0,60 e o coeficiente de atrito ciné
O bloco A da Fig. 6-33 pesa 102N e o bloco B pesa 32N . Os coeficientes de atrito entre A e a rampa são μ s = 0,56 e μ k = 0,25 . O ângulo θ é igual a 40 ° . Suponha que o eixo x é paralelo à rampa, c
Na Fig. 6-34, os blocos A e B pesam 44N e 22N , respectivamente. (a) Determine o menor peso do bloco C que evita que o bloco A deslize, se μ s entre A e a mesa é 0,20 . (b) O bloco C é removido brusca
Uma caixa de brinquedos e seu conteúdo têm um peso total de 180N . O coeficiente de atrito estático entre a caixa de brinquedos e o piso é 0,42 . A criança da Fig. 6-35 tenta arrastar a caixa puxando-
Na Fig. 6-37, uma prancha de massa m 1 = 40k g repousa em um piso sem atrito e um bloco de massa m 2 = 10k g repousa sobre a prancha. O coeficiente de atrito estático entre o bloco e a prancha é 0,60