Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.Problemas - Ex. 72
Uma caixa de encontra-se sobre uma rampa inclinada acima do plano horizontal. O coeficiente de atrito cinético entre a caixa e a rampa é . Que força horizontal é necessária para fazer a caixa subir com uma aceleração constante de ?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a força horizontal é necessária para fazer a caixa subir com uma aceleração constante de . Pra isso, nós sabemos que a caixa tem massa , está sobre uma rampa inclinada de um ângulo e que o coeficiente de atrito cinético entre a caixa e a rampa é .
O primeiro passo sempre é desenhar as forças:
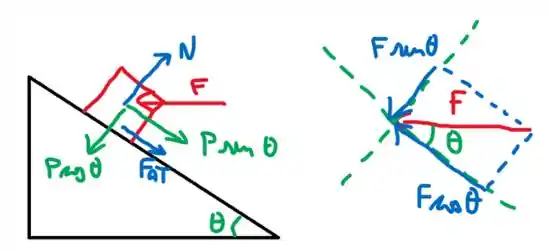
Como o bloco vai subir, o atrito se opõe ao movimento e já desenhei a força peso decomposta. O diferencial desse problema é a força horizontal que decomposta contribui com na direção do movimento e na direção normal!
Então, vamos usar a segunda lei de Newton para analisar as forças atuantes e determinar a força .
Vamos lá!
Passo 2
Na direção normal, temos a componentes verticais:
Já na direção do movimento, vamos ter:
Lembrando que a força de atrito é e a força peso é , segue que:
Passo 3
Vamos isolar na equação:
Logo,
Agora é só substituir os valores:
Com isso, achamos
Valeu, galera! Até a próxima! 😉