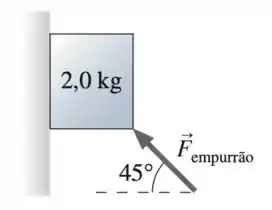
A caixa de madeira de 2,0 kg da figura abaixo desliza verticalmente para baixo sobre uma parede enquanto você a empurra contra ela segundo um ângulo de 45°. Qual é o módulo da força que você deve exercer sobre a caixa a fim de que ela desça com velocidade constante?

Quando o enunciado nos diz que a velocidade é constante, isso sempre é um spoiler que a aceleração é igual a zero. Então, sabemos que a força resultante também tem que dar zero.

E analisando as forças que agem no corpo e adotando o eixo y positivo para baixo, temos que

Já que as forças atuantes são a força gravitacional no sentido do movimento, a força F no eixo y e a força de atrito no sentido contrário ao movimento (por isso negativas). E como a gente quer a F, vamos isolar

E a gente sabe todos esses dados, menos o coeficiente de atrito. Porém, ele foi informado na tabela 6.1 do livro. A partir dela, adotamos µc = 0.2. Vamos substituir!

E assim, concluímos o exercício! ;)