Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 46
Um bloco de madeira de 2,0 kg é lançado rampa acima. Esta é feita de madeira e tem 30° de inclinação com a horizontal. A velocidade inicial do bloco é de 10 m/s.
a. Que altura vertical acima de seu ponto de partida o bloco atingirá?
b. Que valor de velocidade ele terá ao retornar ao ponto de partida?
Passo 1
Fala aí! Essa é um problema de plano inclinado. Se a gente considerar o bloco de madeira como uma partícula quadrada azul, nosso problema vai passar a se parecer com isso:
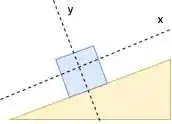
E vamos dar uma olhada nas forças que agem sobre nosso bloquinho.
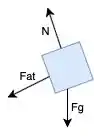
Ok, sabendo disso, a gente precisa ter a sacada que, o ponto máximo do trajeto é quando a velocidade é igual a zero. Podemos calcular quantos metros o bloquinho vai subir até a velocidade ser zero. Vamos recorrer à velha cinemática:
Sabemos a velocidade inicial e a velocidade final. Pra gente descobrir a variação do espaço, só falta a gente saber a aceleração. E pra descobri-la, bora usar a segunda lei de newton!
Passo 2
Olhando para o eixo x (direção e sentido do movimento), temos que a força resultante é dada por
Vamos isolar a aceleração!
E a gente também precisa substituir a força de atrito. Pra isso a gente vai precisar do coeficiente de atrito, que não foi dado no enunciado, mas foi dado em uma tabela em outro lugar do livro:
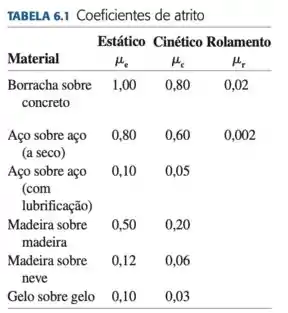
Como o enunciado explicita que tanto a superfície quanto o bloco são de madeira, significa que nosso coeficiente de atrito cinético deve ser 0.2.
Pronto! Agora a gente pode voltar e colocar esse valor na nossa fórmula inicial de cinemática.
Significa que o bloquinho de madeira percorreu 7.6m antes de parar. Mas ainda não é isso que o enunciado tá pedindo! Repara que na letra A o enunciado pede, explicitamente, a distância vertical, e nosso deslocamento calculado faz com a horizontal.
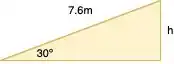
Então, ainda nos resta um último cálculo:
Agora sim, chegamos ao resultado do item A.
Passo 3
Agora, para o item B a gente precisa calcular a velocidade que a madeira vai estar ao retornar para o mesmo ponto inicial. O problema é parecido com o item A, mas agora o nosso diagrama de forças se parece com isso:
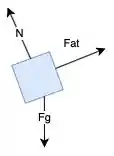
E a gente sabe que o bloco vai descer deslizando por 7.6m(calculado no passo anterior). Porém, a velocidade vai ser diferente, porque dessa vez a aceleração da gravidade está a favor do movimento.
Então, vamos aplicar a fórmula da cinemática novamente!
Porém, sabemos que essa velocidade está no sentido contrário a trajetória. Por isso, seu sinal deve ser negativo.