Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 67
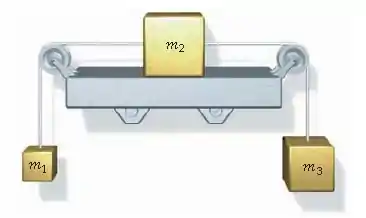
Uma caixa de massa está sobre uma estante horizontal sem atrito e presas por fios a caixas de massas e , como mostra a Figura 4-51. As duas polias são sem atrito e sem massa. O sistema é largado do repouso. Após a largada, encontre (a) a aceleração de cada uma das caixas e (b) a tensão em cada fio.
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar essa questão. Temos uma caixa em cima de uma superfície horizontal. Temos outras duas caixas presas nela. Uma a esquerda e outra a direita.
Só que a caixa a direita é tem massa maior, então quando o sistema é largado do repouso, a tendencia é as caixas serem puxadas pela caixa de maior massa.
Ele começa pedindo a aceleração de cada caixa. É interessante pensar nesses casos onde um objeto puxa o outro, que a aceleração para todos os objetos vai ser a mesma mesma, porque eles se movem juntos com uma distância constante entre eles (a cordinha no nosso caso).
Se eles tivessem acelerações diferentes, por exemplo, se a caixa da direita tivesse maior aceleração, ela ia ter maior rapidez, se afastando da caixa do meio cada vez mais. Mas isso não é possível por causa da cordinha que tem sempre o mesmo comprimento.
Antes de partir para achar essa aceleração, a gente precisa fazer o diagrama de corpo livre de cada caixa para ter ideia de como as forças estão interagindo:
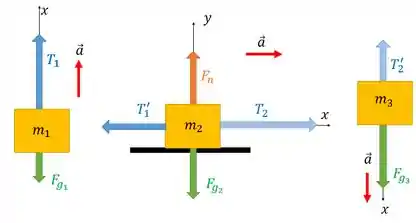
A gente colocou no sentido da aceleração em cada caso só para facilitar as contas. Percebe que a aceleração é resultado de uma força resultante no seu sentido, por isso as força no sentido da aceleração aparecem maiores do que as que estão nos sentido inverso.
Temos tensões onde a gente tem as cordinhas. Cada caixa tem sua força peso por ter massa. E a caixa do meio tem uma força normal por estar em contato com a superfície.
Bora equacionar essas forças através da segunda lei de Newton para achar .
Passo 2
Aplicando a segunda lei de Newton na caixa de massa na direção , temos:
Como está no sentido do eixo , ela aparece positiva no somatório, e o contrário acontece com :
Lembrando que :
Aplicando a segunda lei de Newton na caixa de massa , temos:
Aqui quem está no sentido positivo de é , que fica positiva no somatório e o contrário acontece com :
Como , porque é a mesma corda, temos que:
Aplicando a segunda lei de Newton na caixa de massa , temos:
Aqui quem está no sentido de é a força peso , por isso ela aparece com sinal positivo no somatório, o contrário de (que vai ter o mesmo módulo de ):
Passo 3
Como a aceleração do sistema é igual para todos os corpos, podemos relacionar as equações encontradas:
A gente pode somar todas elas e simplificar:
Isolando quem a gente quer:
Substituindo os valores, temos que:
Passo 4
b) Queremos descobrir e .
Da equação , temos que
Substituindo os valores:
E da equação temos que
Substituindo os dados: