Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 86

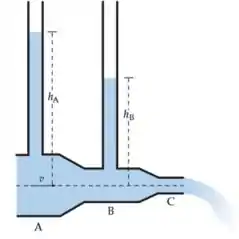
A água flui através do tubo na figura abaixo e sai para a atmosfera na extremidade direita da seção C. O diâmetro do tubo é de 2,00 cm em A, 1,00 cm em B e 0,88 cm em C. A pressão do manômetro na o tubo no centro da seção A é de 1,22 atm e a vazão é de 0,800 L / s. Os tubos verticais estão abertos ao ar. Encontre o nível (acima da linha média do fluxo, como mostrado) das interfaces líquido-ar nos dois tubos verticais. Assuma o fluxo laminar não viscoso.

Passo 1

Essa questão vai parece ser um pouco grande mas calma ela é uma questão de dominar as fórmulas. Mediremos a altura líquido-ar em relação à linha central do tubo e vamos usar a definição da vazão volumétrica em um tubo para encontrar a velocidade da água no ponto A e a relação entre as pressões do medidor nos pontos A e C para determinar o nível da interface ar-líquido em A.

Relacionando a pressão no tubo em A à altura da ar-líquido em A temos:

P g , a =   ρ g h a

h a = P g , a ρ g

Em que h a é medido a partir do centro do tubo. Substituindo os valores encontraremos:

h a = 1.22   a t m 1.01 × 10 5 P a a t m ( 1 × 10 3   k g / m 3 ) ( 9.81   m / s 2 )

h a = 12.6   m

Determinando a velocidade da água em A que será a razão do fluxo pela área:

v a = Q A a = 0.8 × 10 - 3   m 3 s π 4 ( 0.02 m ) 2 = 2.55   m / s

Passo 2

Usaremos a equação de continuidade para expressar a velocidade da água em B em termos de sua velocidade em A e a equação de Bernoulli para elevação constante para encontrar a pressão em B. Aplicando a equação de Bernoulli:

P a + 1 2 ρ v a 2 = P b + 1 2 ρ v b 2

E utilizando a equação de continuidade para relacionar v a e v b :

A a v a = A b v b

v b = A a A b   v a

Substituindo os valores temos:

v b = 2   c m 2 1   c m 2 v a = 4 v a

Substituindo v b na equação de Bernoulli obtemos:

P a + 1 2 ρ v a 2 = P b + 8 ρ v a 2

P b = P a - 15 2 ρ v a 2 = P g , a + P a t - 15 2 ρ v a 2

Agora só falta calcular o P b a partir desse valores já conhecidos:

P b = ( 1.22   a t m + 1   a t m ) ( 101.325 k P a a t m ) - 15 2 ( 1 × 10 3   k g / m 3 ) ( 2.55   m / s ) 2

= 1.762 × 10 5 P a × 1 a t m 101.325 k P a

= 1.739 a t m

Passo 3

Agora que usamos a relação entre as pressões nos pontos A e B, podemos encontrar o nível líquido-ar em B. Relacionando a pressão no tubo em B à altura da ar-líquido em B temos:

P g , b =   ρ g h b

h b = P g , b ρ g = ( P b - P a t ) / ρ g

Substituindo os valores:

h b = ( 1.739 a t m - 1 a t m ) ( 101.325 k P a a t m ) ( 1 × 10 3   k g / m 3 ) ( 9.81   m / s 2 ) = 7.63   m

Resposta

h b = 7.63   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro de 975 kg tem os seus pneus cheios a ’32,0 libras’. (a) Quais são a pressão absoluta e a pressão manométrica nesses pneus em l i b r a s / p o l e g a d a s 2 , P a e a t m ? (b) Se os pneus
14.22a. O tanque em forma de L mostrado na Fig. 14-36 está cheio d’água e é aberto na parte de cima. Se d=5,0m , qual é a força exercida pela água na face A?
23. Um grande aquário de 5,00m de altura está cheio de água doce até uma altura de 2,00m . Uma das paredes do aquário é feita de plástico e tem 8,00m de largura. De quanto aumenta a força exercida sob
Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica 1,30 × 10 ³k g / m ³ . ³ ³ A área de cada base é 4,00c m ² ², mas em um dos recipientes a altura
Um barril contém uma camada de óleo de 0,120 m flutuando sobre a água com uma profundidade igual a 0,250 m. A densidade do óleo é igual a 600k g / m 3 . (a) Qual é a pressão manométrica na interface e