Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.1 - Ex. 6

Uma caixa de massa M começa a se deslocar a partir do repouso, no topo de uma rampa sem atrito e inclinada a um ângulo θ acima da horizontal. Calcule sua velocidade escalar na extremidade inferior da rampa a uma distância d do ponto de partida. Faça isso de duas formas:

(a) Considere que o nível no qual a energia potencial é igual a zero situa-se na extremidade inferior da rampa, com y positivo orientado de baixo para cima.

(b) Considere o nível zero para a energia potencial no topo da rampa, com y positivo orientado de baixo para cima.

(c) Por que a força normal não foi considerada na solução?

Passo 1

Opa, temos uma caixa deslizando do topo de uma rampa. Assim:

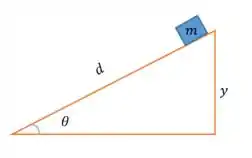
Não temos atrito e a velocidade inicial é igual a zero. Aqui a gente deve calcular a velocidade final depois da caixa percorrer a distância d .

Pra isso primeiro a gente deve considerar que na base da rampa a energia potencial é igual a zero. Ou seja, é a origem do nosso eixo y como geralmente a gente considera em questões assim!

Vamos considerar que a força normal não funciona, então apenas a gravidade funciona, então dá para utilizarmos a seguinte fórmula:

K 1 + U 1 = K 2 + U 2

O problema nos pede a velocidade escalar de duas formas. Inicialmente, será com energia potencial igual a zero na extremidade inferior. Sabendo que nessa mesma extremidade da rampa tem uma distância d no ponto de partida, então

y 1 = d sin ⁡ θ

Tendo o y positivo, então

y 2 = 0

Consequentemente, U 1 = K 2 . K 1 = 0 , pois não há movimentação inicial.

Calculando...

m g y 1 = 1 2 m v 2 2

m g d sin ⁡ θ = 1 2 m v 2 2

Logo,

g d sin ⁡ θ = 1 2 v 2 2

2 g d sin ⁡ θ = v 2 2

v 2 = 2 g d sin ⁡ θ

Passo 2

Se o nível zero para a energia potencial no topo da rampa, teremos outra configuração, onde

y 1 = 0

E,

y 2 = - d sin ⁡ θ

Então,

K 1 + U 1 = K 2 + U 2

0 = K 2 + U 2

Substituindo temos,

0 = 1 2 v 2 2 - m g d sin ⁡ θ

v 2 2 = m g d sin ⁡ θ

v 2 = 2 g d sin ⁡ θ

Igual ao item (a).

Passo 3

“Ta, mas eu não entendi foi nada. Porque a normal não foi considerada?”.

Lá nos conceitos básicos da física, sabemos que a normal é uma perpendicular ao deslocamento, certo?? Por isso mesmo, ela não contribui para o trabalho (W).

Prontinho!

Resposta

a) v 2 = 2 g d sin ⁡ θ

b) v 2 = 2 g d sin ⁡ θ

c) A normal não contribui para o trabalho.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quanta energia é necessária para mover um corpo com 1 000 kg a partir da superfície da Terra a uma altitude igual a duas vezes o raio da Terra?
Uma pedra de 0,20k g é mantida 1,3m acima da borda superior de um poço e depois derrubada dentro dele. O poço tem uma profundidade de 5,0m . Em relação à configuração com a pedra na borda superior do
Um carrinho de montanha-russa de 1000k g está inicialmente no topo de uma subida, no ponto A. Ele então se move 135p é s é , a um ângulo de 40,0 ° abaixo da horizontal até um ponto mais baixo B. Consi
1 . Um bate-estaca, nivelado com o solo, bate repetidamente um corpo pesado. Suponha que o corpo seja lançado da mesma altura todas as vezes. Por qual fator a energia do sistema bate-estaca-Terra muda
Que potência média é gerada por um alpinista de 70,0 kg que escala um pico de altura 325 m em 95 min?a.39,1 Wb.54,6 Wc.25,5 Wd.67,0 We.88,4 W