Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.1 - Ex. 3

Uma mala postal de 120   k g é suspensa por uma corda vertical de 3,5   m de comprimento. Um funcionário desloca a mala lateralmente para uma posição 2,0   m da sua posição original, sempre mantendo a corda esticada.

a) Qual é o módulo da força necessária para manter a mala na nova posição?

b) Para deslocar a mala até essa posição, qual é o trabalho realizado (i) pela corda e (ii) pelo funcionário?

Passo 1

Opa, bora lá! Temos um objeto de 120     k g preso verticalmente por uma corda de 3,5   m até uma pessoa mover esse objeto 2 metros horizontalmente. Ou seja:

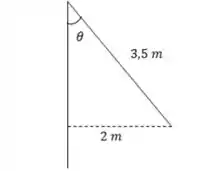
Primeiro queremos saber a força necessária para manter a mala na nova posição.

Então, galera, o que vamos precisar aqui? A mala está sendo deslocada e ela tende a permanecer em repouso no inicio e no final, né não? “Mas o que é isso?” Primeira lei do nosso amigo Newton:

E c = 0   e   W = 0

Pelo enunciado temos uma corda na posição vertical mais um deslocamento lateral, essa representação gera um ângulo que vai ser seno. Vemos:

sin ⁡ θ = c . o h i p

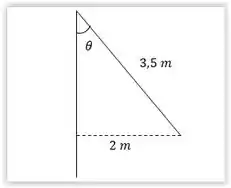
O deslocamento é o c.o, logo

sin ⁡ θ = 2   m 3,5   m

θ = 34,85 °

Temos tudo que precisamos, vamos calcular as forças envolvidas na vertical, mais conhecido como eixo y .

Passo 2

Agora utilizamos o diagrama de forças,

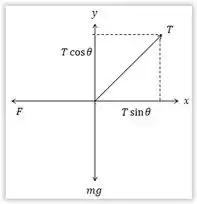
Fazendo o somatório de forças temos:

∑ F y = 0

T cos ⁡ θ = m g

No eixo x, temos

∑ F x = 0

F = T sin ⁡ θ

Agora é só igualarmos as equações,

T = m g cos ⁡ θ e T = F sin ⁡ θ

F sin ⁡ θ = m g cos ⁡ θ

F = m g sin ⁡ θ cos ⁡ θ

Logo,

F = m g tan ⁡ θ

F = ( 120   k g ) ( 9,8   m / s 2 ) tan ⁡ 34,85 °

F = 820   N

Prontíssimo, agora vamos para a letra (b).

Passo 3

Agora queremos saber o trabalho da mala no deslocamento e o trabalho realizado pela corda.

Bom, a tensão na corda correspondente ao centro (radial), porém o deslocamento é tangencial, certo? Ou seja, ele é pouco relevante. Logo, durante o movimento, não há nenhum componente de tensão T , o que anula o funcionamento da tensão na corda e não produz trabalho.

Agora, pelo funcionário, já sabemos que o trabalho total é zero (Passo 1 ). A única força atuante no movimento é a da gravidade, logo

W = U 2 - U 1

W = m g y 2 - m g y 1

W = m g ( y 2 - y 1 )

W = ( 120   k g ) ( 9,8   m / s 2 ) ( y 2 - y 1 )

Hum... e o deslocamento vertical? Inicialmente, falamos que o c.o seria 2   m e a hipotenusa 3,5   m , o cateto adjacente vai nos levar a y

a 2 = b 2 + c 2

( 3,5   m ) 2 = ( 2 ) 2 + c 2

c 2 = 8,25

c = 2,872

Porém, sabemos que a corda estica até um certo ponto, então subtraímos,

3,5 - 2,872 = 0,628

Esse vai ser nosso y 2 - y 1 . Substituindo,

W = ( 120   k g ) ( 9,8   m / s 2 ) ( 0,628   m )

W = 740   J

Prontinho!

Resposta

a) F = 820   N

b) Não produz trabalho; W = 740   J .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma explosão no nível do solo produz uma cratera com um diâmentro proporcional à raiz cúbica da energia da explosão; uma explosão de 1m e g a t o n de TNT deixa uma cratera de 1k m de diâmetro. Sob o
Dois ascetas, à procura do conhecimento, decidem subir uma montanha. Silvino escolhe uma trilha curta e muito íngreme, enquanto Joselito escolhe uma trilha longa e suavemente íngreme. No topo, eles di
7 . Energia humana versus energia de inseto. Para seu tamanho, a pulga comum é um dos saltadores mais talentosos do mundo animal. Uma pulga de 2,0m m e 0,50m g podeatingir uma altura de 20c m em um ún
Uma caixa vazia desliza para baixo de uma rampa, começando com uma velocidade inicial v 0 e atingindo a base com uma velocidade v e uma energia cinética K. Alguns livros são colocados no interior da c
Um bloco de gelo de 0,150 kg é colocado contra uma mola horizontal comprimida no alto de uma mesa de altura 1,20 m acima do solo . A mola está inicialmente comprimida 0,045 m e aconstante da mola é ig