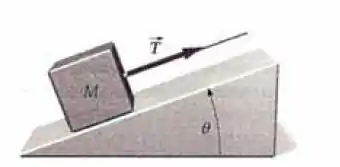
Uma caixade massa M estå em repouso na base de um plano inclinado sem atrito (figura abaixo). A caixa está presa a um fio que a puxa com uma tensão constante T. (a) Determine o trabalho realizado pela tensão T, enquanto a caixa é puxada por uma distância x ao longo do plano. (b) Determine a rapidez da caixa como função de x. (c) Determine a potência desenvolvida pela tensão do fio como função de x.

Letra (b)

Pelo teorema do trabalho-energia, temos:

Como a caixa parte do repouso:

Agora a gente isola o :

Agora precisamos achar o. O que a gente achou na letra (a) é só devido à tensão. Mas o trabalho devido ao peso é:

O trabalho total é dado por

Jogando esse trabalho na velocidade:

Letra (c)

A potência é dada por:

A força é e a velocidade a gente achou na letra (b):