Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 76

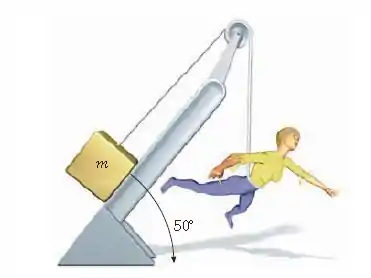
Durante uma apresentação teatral de Peter Pan, a atriz de 50   k g que representa Peter Pan deve voar verticalmente (descendo). Para acompanhar a música ela deve, a partir do repouso, ser baixada de uma distância de 3,2   m em 2,2   s com a celeração constante. Nos bastidores, uma superfície lisa inclinada de   50 ° suporta um contrapeso de massa m , como mostrado na Figura 4-55. Mostre os cálculos que o operador deve fazer para encontrar (a) a massa de contrapeso a ser usada e (b) a tensão no fio.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

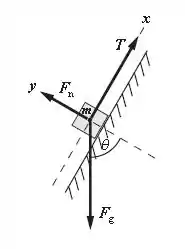
O diagrama de corpo livre, para a situação descrita, está exposto abaixo:

Passo 2

Aplicando a segunda lei de Newton no objeto de massa m 1 , que é o contrapeso, temos:

∑ F x = m a x

T - m 1 g sin ⁡ 50 ° = m 1 a x

Aplicando a segunda lei de Newton no objeto de massa m p , temos:

∑ F x = m a x

m p g - T = m p a x

Logo:

m 1 = m p g - a x a x + g sin ⁡ 50 °

Sabemos que a x = 2 ∆ x ∆ t 2

m 1 = m p g - 2 ∆ x ∆ t 2 2 ∆ x ∆ t 2 + g sin ⁡ 50 °

Substituindo por valores, temos:

m 1 = 50 9,81 - 2 ⋅ 3,2 2,2 2 2 ⋅ 3,2 2,2 2 + 9,81 sin ⁡ 50 °

m 1 = 48   k g

Passo 3

A tensão será:

T = m 1 ( a x + g sin ⁡ 50 ° )

T = 48 2 ⋅ 3,2 2,2 2 + 9,81 sin ⁡ 50 °

T = 0,42   k N

Resposta

a ) m 1 = 48   k g

b ) T = 0,42   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma artista amiga sua precisa de ajuda para pendurar uma escultura de 500 lb no teto. Por razões artísticas, ela deseja usar apenas duas cordas. Uma delas deverá formar 30° com a vertical, e a outra,
Um acelerômetro simples é construído dentro de um carro suspendendo-se um corpo de massa m de um fio de comprimento L que está preso ao seu teto. À medida que o carro acelera, o fio – o sistema do cor
Um saco de cimento cujo peso é F g está pendurado em equilíbrio por três cabos, como mostrado na Figura P4.23. Dois dos cabos formam ângulos θ 1 e θ 2 com a horizontal. Supondo que o sistema esteja em
A Figura P4.26 mostra cargas penduradas no teto de um elevador que está se movendo em velocidade constante. Encontre a tensão em cada uma das três vertentes da corda que sustenta cada carga.
Um saco de cimento pesando 325N está pendurado em equilíbrio por três cabos, como sugerido na Figura P4.23. Dois dos cabos formam ângulos θ 1=60,0 ° e θ 2=40,0 ° com a horizontal. Supondo que o sistem