Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 41
Um caixote, na forma de um cubo com de lado contém uma peça de máquina; o centro de massa do caixote e do conteúdo está localizado acima do centro geométrico do caixote. O caixote repousa em uma rampa que faz um ângulo com a horizontal. Quando aumenta a partir de zero, um valor de ângulo é atingido para o qual o caixote tomba ou desliza pela rampa. Se o coeficiente de atrito estático entre a rampa e o caixote é , (a) o caixote tomba ou desliza? (b) Para que ângulo isso acontece? Se , (c) o caixote tomba ou desliza? (d) Para que ângulo isso acontece? (Sugestão: qual é o ponto de aplicação da força normal quando o caixote está prestes a tombar?)
Passo 1
(a)Show de bolinhas pessoal, pra ficar mais fácil pra gente, vamos desenhar a situação ilustrada no problema para ajudar no nosso raciocínio. Primeiro vamos focar no momento em que o caixote está prestes a tombar. Quando isso acontece, a força normal estará sendo aplicada sobre a aresta inferior que servirá de eixo de rotação, assim como indicamos na figura.
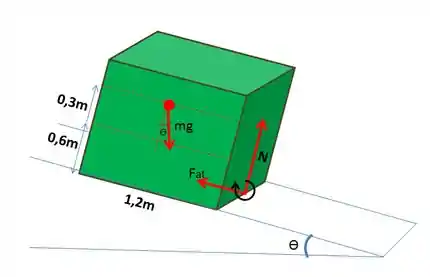
Onde é força de atrito relacionada a força normal .
Passo 2
Iradoso, vamos agora analisar o que deve acontecer para que o caixote não deslize. Para isso, devemos ter um equilíbrio de forças na direção da superfície da rampa. Quando isso não acontece, ele passa a deslizar com uma força resultante na direção de . Nesse caso, a gente tem:
Além disso, como o bloco está em equilíbrio na direção normal à rampa, temos:
Substituindo esse valor na equação , obtemos
Então:
Ou seja, a partir do ângulo o bloco passa a deslizar ao longo da rampa.
Passo 3
Agora, vamos analisar o equilíbrio de torques com relação ao centro de massa (onde é aplicada a força peso ). Esse equilíbrio deve ocorrer para que o caixote não tombe. Caso o plano seja gradualmente inclinado para cima e vá aumentando, vai chegar um momento em que o bloco tenda a girar (tombar) para a direita, quando o somatório dos torques passa a ser positivo. A equação que representa isso é a seguinte:
No caso em que o bloco tomba sem deslizar, a resultante das forças na direção da rampa é zero, assim como na direção normal à sua superfícir. Então: e . Nesse caso:
Então, como , temos que a partir desse ângulo o bloco tomba sem deslizar. Como esse ângulo é maior do que o encontrado anteriormente (), podemos concluir que o caixote desliza antes de querer tombar.
Passo 4
(b)Como vimos no passo 2, o bloco só passa a deslizar para ângulos maiores que .
Passo 5
(c)Aqui, vamos substituir na expressão encontrada no passo 2. Assim, temos que o caixote começa a deslizar a partir de
.
Além disso, como vimos no passo 3, o caixote começa a tombar quando , ou seja, . Isso quer dizer que nesse caso ele tomba antes de deslizar.
Resposta
(a)Desliza antes de tombar
(b)Começa a deslizar para
(c)Tomba antes de deslizar
(d)