Na Figura, uma prancha homogênea, com comprimento de e peso de , repousa apoiada no chão e em um rolamento sem atrito no alto de uma parede de altura . A prancha permanece em equilíbrio para qualquer valor de , mas escorrega se . Determine o coeficiente de atrito estático entre a prancha e o chão.

Antes é bom lembrar que F precisa ser decomposta em duas direções, pra ajudar a gente enxergar eu fiz esse desenho:

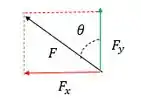
Daí a gente vê que:

E

Logo as duas equações de equilíbrio de forças serão:

Para o somatório dos torques, vamos escolher o ponto onde estão agindo a força normal e a força de atrito, visando eliminar essas incógnitas. Aqui a gente só tem que se ligar que a força P não está perpendicular a barra, a gente pode analisar a decomposição fazendo um desenho:

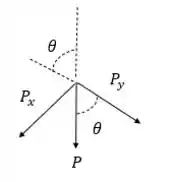
Aí fica mais fácil de ver que:

Onde x é a distância em que F é aplicada.

Beleza, agora mãos á obra pra encontrarmos quem a gente precisa, vamos começar encontrando o valor de F, com a equação 3:

Mas como a gente calcula esse x? É mais de boa do que parece, da barra a gente pode tirar um triângulo, com h e d mostrados na figura.

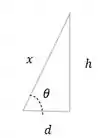
Daí, de boas:

E substituindo:

Rearrumando lá em cima:

E substituindo temos:

Bom, já eliminamos uma incógnita vamos seguir assim pra equação 2, e aí encontraremos a força normal.

Isolando a força normal a gente tem:

Substituindo:

E por último, podemos partir pra equação 1, e encontrar a fat:

Substituindo:

E por fim, a gente pode lembrar que:

Logo: