Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 35
Uma caixa cúbica está cheia de areia e pesa . Deseja-se "rodar" a caixa, empurrando horizontalmente uma de suas arestas superiores. (a) Qual é a força mínima necessária? (b) Qual é o coeficiente de atrito estático mínimo necessário.(c)Se existe um modo mais eficiente de fazer a caixa rolar, determine a menor força possível que deve ser aplicada diretamente à caixa para que isso aconteça.
Passo 1
Primeiro, vamos imaginar o que acontece no problema: suponhamos que estamos aplicando uma força crescente sobre a borda superior do cubo. Conforme aumentamos ela, a força normal exercida pelo solo sobre ele também aumenta e, na iminência de ele girar, essa força está sendo exercida sobre o vértice inferior mais afastado, assim como mostra a figura:
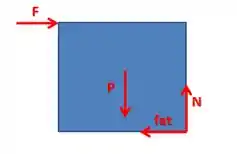
Belezinha, agora que a gente sabe como as forças estão atuando, vamos ver como fica o resto da brincadeira.
Passo 2
Considerando o equilíbrio de torques com relação ao eixo onde são aplicadas e (força de atrito estático), de forma que estas se anulem, obtemos um equilíbrio dado como:
Então:
Logo:
Passo 3
(b)Do equilíbrio na horizontal, vem:
Então:
Passo 4
(c)Essa é uma boa pergunta . Para respondê-la, vamos considerar um caso geral, de uma força aplicada formando um ângulo com a horizontal já que podemos rolar o corpo com uma força aplicada menor nesse caso.
Assim, a equação de equilíbrio de torques passa a ser essa:
Então, temos que:
Para conseguirmos tombar o cubo com a menor possível, temos que minimizar o denominador dessa fração! Como faremos isso?
Passo 5
Aqui, vamos lembrar que . Isso se maximiza quando , ou seja, Então, a força mínima acima é dada por:
Portanto:
Então, a resposta para essa pergunta é: Sim, existe um modo mais eficiente para se rolar o cubo, sem precisar aplicar uma força maior que .
Resposta
(a)
(b)
(c)