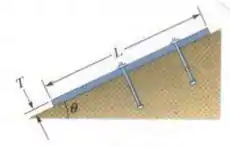
Na figura, uma placa retangular de ardósia repousa em uma superfície rochosa com uma inclinação . A placa tem um comprimento , uma espessura , uma largura e da placa tem uma massa de . O coeficiente de atrito estático entre a placa e a rocha é . (a) Calcule a componente da força gravitacional que age sobre a placa paralelamente à superfície da rocha. (b) Calcule o módulo da força de atrito estático que a rocha exerce sobre a placa. Comparando (a) e (b), você pode ver que a placa corre o risco de escorregar. Isso é evitado apenas pela presença de protuberâncias na rocha. (c) Para estabilizar a placa, pinos devem ser instalados perpendicularmente à superfície da rocha (dois desses pinos são mostrados na figura). Se cada pino tem uma seção reta de e se rompe ao ser submetido a uma tensão de cisalhamento de , qual é o número mínimo de pinos necessário? Suponha que os pinos não alteram a força normal.

Vamos pensar no que a questão pede primeiro: a componente da força gravitacional que age sobre a placa paralelamente à superfície da rocha.

Olha, a gravidade é uma força, e a força é um vetor. Você deve saber que um vetor pode ser “decomposto” em componentes: ou seja, outros vetores que, quando somados vetorialmente, dão o vetor original.

No caso, essa é uma questão clássica de plano inclinado, como é sempre visto na física I. Sabemos que a componente “paralela à superfície da rocha” é só:

Não temos a massa da placa inteira, mas temos a densidade e o volume, e como e

Pronto, essa é a componente do vetor que é paralelo à superfície da rocha.

A letra (b) quer o módulo da força de atrito estático que a rocha exerce sobre a placa.

Vamos lembrar do seguinte: o atrito estático é aquele que impede o objeto de entrar em movimento, o atrito que age para frear o movimento é o atrito cinético.

A questão já deu o coeficiente de atrito estático entre a placa e a rocha, então é só substituir na fórmula:

Onde é o módulo da força normal.

Vamos lembrar também que, no plano inclinado, a força normal é igual à componente vertical do peso, ou seja:

Voltando à fórmula de cima:

Resolvido.

Por último, a letra (c) diz o seguinte: a placa precisa de pinos pra ficar presa na rocha (não deslizar), esses pinos tem uma seção reta de , e aguentam uma tensão de cisalhamento de .

Agora vamos pensar o seguinte: quem está ajudando a placa a ficar presa na rocha? E quem está querendo empurrá-la ladeira abaixo?

Bem, empurrando ladeira abaixo temos a força gravitacional de sempre, que já calculamos, e é .

E ajudando a manter, temos a força de atrito estático () mais a ajuda desses pinos, que vamos calcular.

Beleza, se a placa vai ficar parada, esses dois “times” tem que ter a mesma força, ou seja:

Portanto, a força total feita pelos pinos tem que ser de:

Agora vamos pensar, a fórmula que usamos para a tensão logo acima também, vale para a tensão de cisalhamento:

E essa tensão por pino tem que ser menor do que .

Isso quer dizer que vamos precisar de pinos, para que a força seja bem dividida entre eles:

Como

Como o número de pinos tem que ser inteiro, precisamos de, no mínimo, 16 pinos.