A figura 29-79 mostra uma seção reta de um condutor cilíndrico longo de raio que contrém um furo cilíndrico de raio . Os eixos centrais do cilindro e do furo são paralelos e estão separados por uma distância ; uma corrente está distribuída uniformemente na região sombreada. (a) Determine o módulo do campo magnético no centro do furo

A lei de Àmpere é utilizada para determinar o campo magnético total de uma região que apresente algum tipo de simetria. De acordo com ela:

O círculo do sinal de integral indica que a integração do produto escalar deve ser realizada para uma curva fecahda, conhecida como amperiana. A corrente é a corrente total envolvida pela curva fechada. Essa corrente tamém pode ser escrita como:

,

onde é a densidade de corrente na curva fechada.

Para determinarmos o campo magnético em pontos situados no interior do fio, podemos usar uma amperiana de raio por dentro do fio, conforme a figura abaixo.

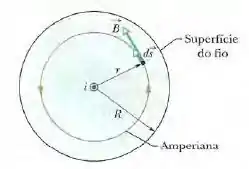
Da lei de Àmpere:

Para calcular o lado direito da lei de Àmpere, observamos que, como a distribuição de corrente é uniforme, a corrente envolvida pela amperiana é proporcional à área envolvida pela curva, ou seja,

Usando a regra da mão direita, vemos que o sinal de é positivo e, portanto, de acordo com a lei de Àmpere,

O campo magnético em um ponto do interior do furo pode ser considerado como a soma dos campos produzidos por duas correntes: a corrente produzida por um cilindro sem o furo e uma corrente, no sentido contrário, produzida por um cilindro de dimensões iguais às do furo. O campo produzido no interior de um cilindro no interior de um cilindro sem fura a uma distância do eixo do cilindro é dado por:

na qual é o raio do cilindro. No caso do cilindro que estamos considerando, a densidade de corrente é:

Assim, a corrente no cilindro sem furo é:

e o módulo do campo produzido em um ponto no interior do cilindro, a uma distância do eixo, é

A corrente em um cilindro com as mesmas dimensões que o furo é:

e o módulo do campo produzido em um ponto interior do cilindro, a uma distância do eixo, é:

No centro do furo, o campo é zero e o campo nesse ponto é o mesmo que em um cilindro sem o furo. Fazendo na expressão de , obtemos o campo no centro do furo:

Se o sentido da corrente na fiigura 29-79 é para fora do papel, o campo aponta para cima.