Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 31.1 - Ex. 46
Calcule a diferença em tempo necessária para que dois pulsos de luz percorram da fibra descrita no problema 44. Considere que um pulso entra na fibra com incidência normal e que o segundo pulso entra na fibra com o ângulo máximo de incidência calculado no problema 45. Na fibra óptica, este efeito é conhecido como dispersão modal.
Passo 1
E aí bonit@s, como vocês estão?
Se liguem só, para nossa fibra óptica do problema podemos montar uma expressão para a diferença nos tempos de viagem expressando o tempo de viagem para um pulso que entra na fibra no ângulo máximo de incidência e um pulso que entra na fibra na incidência normal. Dessa forma teremos que a diferença nos tempos de viagem é dada por
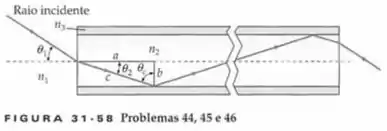
Além disso, ao examinarmos nossa imagem podemos perceber que se o comprimento do nosso tubo for , a distância percorrida pelo pulso que entra no ângulo máximo é a razão entre a velocidade da luz, , multiplicada por . Dessa forma, o tempo de viagem para o pulso que entra na fibra no ângulo máximo de incidência é:
Já o tempo de viagem para o pulso que entra na fibra com ângulo normal é:
Sendo assim, nossa diferença de tempo será
Passo 2
Então meus camaradas, deem uma respirada e voltem aqui. Olha só, novamente olhando para a figura encontramos que
Além disso, pela lei de Snell o seno do ângulo crítico é dado por
Igualando com encontramos
Substituindo em vamos encontrar
Pronto, para finalizar o problema é só substituir os valores numéricos, dado que no problema temos: e assim obteremos
Pronto, tá resolvido a questão sem muito problema.