Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 10.Problemas - Ex. 6

Calcule a impedância do circuito da figura entre os pontos 1 e 2 à frequência ω e mostre que, se as constantes de tempo τ C e τ L forem iguais, a impedância será independente da frequência.

Passo 1

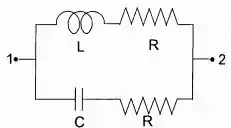
Para resolvermos, vamos separar o sistema em dois: para o percurso de cima, contendo L R e para o sistema de baixo, contendo C R . Colocando os sistemas lado a lado, vamos ver que eles podem ser interpretados como sistemas em paralelo, assim teremos que aplicar a impedância para sistemas em paralelo.

Passo 2

Bom, vamos começar separando os dois sistemas. Podemos interpretar como um sistema L R e um C R estando em paralelo. Com isso, vamos precisar inicialmente calcular a impedância indutiva e capacitiva. Para o sistema L R , temos:

Z L = R + X L

E para o sistema C R vamos ter:

Z C = R + X C

Como vimos no livro, a capacitância indutiva e capacitiva são definidas como:

X C = - i ω C

X L = i ω L

Se calcularmos agora para o conjunto completo do sistema, assumindo que ambos podem ser interpretados como estando em paralelo, teremos que:

1 Z = 1 Z L + 1 Z C = 1 R + i ω L + 1 R - i ω C

Se lembrarmos agora que as constantes de tempo τ C e τ L são definidas como:

τ C = R C

τ L = L R

Temos que ao igualarmos, chegaremos que R 2 = L C . Substituindo na nossa equação para a impedância, vamos ter que

1 Z = 1 L C + i ω L + 1 L C - i ω C = C L

Resposta

1 Z = 1 R + i ω L + 1 R - i ω C = C L ,     p a r a   τ C = τ L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para que frequência um indutor de 6,0m H e um capacitor de 10μ F têm a mesma reatância? (b) Qual é o valor da reatância? (c) Mostre que a frequência é a frequência natural de um circuito com os mesmos
Um gerador de corrente alternada com uma força eletromotriz ε = ε Ms e nω d t - π 4 , onde ε M = 30 , 0V e ω d = 3 50r a d / s . A corrente produzida no circuito ao qual o gerador está ligado é i t =
Um resistor de 50,0Ω é ligado, como na Fig. 31-8, a um gerador de corrente alternada com ε M = 30,0V . Determine a amplitude da corrente alternada resultante se a frequência da força eletromotriz for
Um indutor de 50,0m H é ligado, como na Fig. 31-12, a um gerador de corrente alternada com ε M = 30,0V . Determine a amplitude da corrente resultante se a frequência da força eletromotriz for (a) 1,00
Um gerador de corrente alternada com uma força eletromotriz ε = ε Ms e nω d t , onde ε M = 25,0V e ω d = 377r a d / s é ligado a um capacitor de 4,15μ F . (a) Qual é o valor máximo da corrente? (b) Qu