Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 10.Problemas - Ex. 8
No circuito da figura, . Calcule a frequência angular de ressonância definida como o valor de para o qual a reatância do circuito se anula.
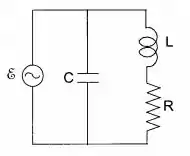
Passo 1
Nesse problema iremos utilizar as relações para encontrar a frequência de ressonância para o caso onde as reatâncias se anulam. Para isso, vamos primeiro achar a impedância do circuito e a partir daí iremos analisar o caso em que as reatâncias se anulam e apenas resta a resistência.
Passo 2
Bom, como dito no passo 1, vamos começar achando a impedância para o circuito em paralelo, assim como mostrado no livro. Temos que a impedância para a resistência e o indutor é dada por:
Agora para a capacitância, vamos ter que o circuito estará em paralelo, assim a impedância total do circuito se dá por:
Queremos que apenas reste a resistência, então para conseguirmos deixar apenas esse termo existente, temos que satisfazer a seguinte relação:
Sendo essa nossa frequência para o qual todas as reatâncias se anulam, tornando a resistência do circuito a mínima possível e fazendo com que o sistema fique com a maior frequência de oscilação possível.